Question 179343: Can you please help me solve this radical equaqtion? 
This problem did not come from a text book, it came from a worksheet.
I began by isolating the radical: 
Then I squared each side to eliminate the radical: 
Which gave me: 
Then I moved everything to one side to give me a quadradtic equation:

This is where I got stuck, I don't see how this can be factored, so I tried using the quadratic equation and just got confused from there. Can you help me please??!!???
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can you please help me solve this radical equaqtion? 
This problem did not come from a text book, it came from a worksheet.
I began by isolating the radical: 
Then I squared each side to eliminate the radical: 
Which gave me: 
There's your error!
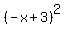 IS NOT IS NOT 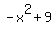 ! !
When there are two terms added to be squared, you must
write it in parentheses TWICE and multiply it by itself,
using FOIL. Also you must remember that when you square
a negative, such as 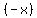 you get a positive you get a positive 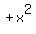 ,
not ,
not  :
Therefore when you got to :
Therefore when you got to
 the next step should have been
the next step should have been
 Then you must use "FOIL":
Then you must use "FOIL":

 You don't need to write that
You don't need to write that  . I just
put it there to remind you that when you square
a negative you get a positive. . I just
put it there to remind you that when you square
a negative you get a positive.

 Then move everything right and you get:
Then move everything right and you get:
 or if you like the 0 on the right, just swap sides:
or if you like the 0 on the right, just swap sides:
 Then it factors nicely as
Then it factors nicely as
 Then you get the solutions
Then you get the solutions  and and  But you must check these, because when you square
both sides or multiply both sides by a variable,
you may get extraneous solutions:
Checking
But you must check these, because when you square
both sides or multiply both sides by a variable,
you may get extraneous solutions:
Checking 




 That doesn't check, so
That doesn't check, so  is not a
genuine solution, but is called "extraneous".
Checking is not a
genuine solution, but is called "extraneous".
Checking 




 That checks. So
That checks. So  is the only solution
Edwin is the only solution
Edwin
|
|
|