SOLUTION: 1. Find the equation of a straight line that passes through a point (–1,3) such that it is perpendicular to straight line y - 2x = 5. 2. Sketch a graph for a quadratic function

Algebra ->  Linear-equations -> SOLUTION: 1. Find the equation of a straight line that passes through a point (–1,3) such that it is perpendicular to straight line y - 2x = 5. 2. Sketch a graph for a quadratic function      Log On


   

Question 178329: 1. Find the equation of a straight line that passes through a point (–1,3) such that it is perpendicular to straight line y - 2x = 5.
2. Sketch a graph for a quadratic function given as below:
f (x) = x² - x - 6
Found 2 solutions by jojo14344, stanbon:
Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!

1)We have to remember when 2 lines are perpendicular, the slope=m%5B2%5D of the other one is "negative reciprocal" of the 1st :------>m2=-1%2Fm%5B1%5D
Arranging Line 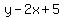y-2x%2B5 via Slope-intercept form, y=mx%2Bb:
y=2x%2B5
We can see it has a Slope=m%5B1%5D=2, then the line that passes thru point (-1,3) has a slope:
m%5B2%5D=-1%2F2
Via Slope-intercept Form: point (-1,3)
3=%28-1%2F2%29%28-1%29%2Bb
3=%281%2F2%29%2Bb---->b=3-%281%2F2%29=%286-1%29%2F2=5%2F2, Y-Intercept
Therefore, line eqn. y=%28-1%2F2%29x%2B%285%2F2%29 ----> y%2B%281%2F2%29x=5%2F2 (Standard form) passes thru point (-1,3) and perpendicular to line y-2x=5
we'll see:
-----> RED Line>>>> y=2x%2B5; GREEN Line>>>> y%2B%281%2F2%29x=5%2F2
.
2)Sketch a graph for a quadratic function given as below:
f+%28x%29+=+x%B2+-+x+-+6
Solving the quadratic:
x%5E2-x-6=0
wheresystem%28a=1%2Cb=-1%2Cc-6%29

x=%281%2B-sqrt%281%2B24%29%29%2F2=%281%2B-sqrt%2825%29%29%2F2
x=%281%2Bsqrt%2825%29%29%2F2=%281%2B5%29%2F2=6%2F2=highlight%283%29
x=%281-sqrt%2825%29%29%2F2=%281-5%29%2F2=-4%2F2=highlight%28-2%29
X-intercepts--------> (3,0) & (-2,0)

Thank you,
Jojo

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
1. Find the equation of a straight line that passes through a point (–1,3) such that it is perpendicular to straight line y - 2x = 5.
-----------
The slope of the given line is 2 because y = 2x+5
-----------------------------------
The perpendicular line must have slope = -1/2
--------------------
Intercept: 3 = (-1/2)*-1 + b; b = = 3 - 1/2 = 5/2
--------------------------
Equation: y = (-1/2)x + (5/2)
==================================
Cheers,
Stan H.





2. Sketch a graph for a quadratic function given as below:
f (x) = x² - x - 6