SOLUTION: I have been struggling to figure out this math problem and I was wondering if someone could help me? Please and Thank You!! I would deeply appreciate it!! Binomials Containing R

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I have been struggling to figure out this math problem and I was wondering if someone could help me? Please and Thank You!! I would deeply appreciate it!! Binomials Containing R      Log On


   

Question 178268This question is from textbook Algebra and Trigonometry Structure and Method book 2
: I have been struggling to figure out this math problem and I was wondering if someone could help me? Please and Thank You!! I would deeply appreciate it!!
Binomials Containing Radicals
Simplify. Assume that each radical represents a real number.
(√(n+1) +√n)( √(n+1) -√n) This question is from textbook Algebra and Trigonometry Structure and Method book 2

Found 3 solutions by jim_thompson5910, EMStelley, Alan3354:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
When trying to simplify or expand complicated expressions involving roots, you can try substitutions to get the expression into a cleaner form (it's not required, but I find that it helps you see the big picture).


So if we let x=sqrt%28n%2B1%29 and y=sqrt%28n%29, we can simplify


%28sqrt%28n%2B1%29%2Bsqrt%28n%29%29%28sqrt%28n%2B1%29-sqrt%28n%29%29


to get


%28x%2By%29%28x-y%29 (note: I just replaced every sqrt%28n%2B1%29 with "x" and every sqrt%28n%29 with "y")


---------------------------------------------------



Now let's FOIL %28x%2By%29%28x-y%29


Remember, when you FOIL an expression, you follow this procedure:


%28highlight%28x%29%2By%29%28highlight%28x%29-y%29 Multiply the First terms:%28x%29%2A%28x%29=x%5E2.


%28highlight%28x%29%2By%29%28x%2Bhighlight%28-y%29%29 Multiply the Outer terms:%28x%29%2A%28-y%29=-x%2Ay.


%28x%2Bhighlight%28y%29%29%28highlight%28x%29-y%29 Multiply the Inner terms:%28y%29%2A%28x%29=x%2Ay.


%28x%2Bhighlight%28y%29%29%28x%2Bhighlight%28-y%29%29 Multiply the Last terms:%28y%29%2A%28-y%29=-y%5E2.


---------------------------------------------------


x%5E2-x%2Ay%2Bx%2Ay-y%5E2 Now collect every term to make a single expression.


x%5E2-y%5E2 Now combine like terms.


So %28x%2By%29%28x-y%29 FOILs to x%5E2-y%5E2.


In other words, %28x%2By%29%28x-y%29=x%5E2-y%5E2.


---------------------------------------------------------


%28x%2By%29%28x-y%29=x%5E2-y%5E2 Start with the last equation


Plug in x=sqrt%28n%2B1%29 (ie replace every "x" with sqrt%28n%2B1%29)


Plug in y=sqrt%28n%29 (ie replace every "y" with sqrt%28n%29)


Simplify


Square sqrt%28n%2B1%29 to get n%2B1 (note: the square undoes the square root)


%28sqrt%28n%2B1%29%2Bsqrt%28n%29%29%28sqrt%28n%2B1%29-sqrt%28n%29%29=n%2B1-n Square sqrt%28n%29 to get n (note: the square undoes the square root)


%28sqrt%28n%2B1%29%2Bsqrt%28n%29%29%28sqrt%28n%2B1%29-sqrt%28n%29%29=1 Combine like terms.



=====================================================================

Answer:


So %28sqrt%28n%2B1%29%2Bsqrt%28n%29%29%28sqrt%28n%2B1%29-sqrt%28n%29%29=1

Answer by EMStelley(208) About Me  (Show Source):
You can put this solution on YOUR website!
If you remember, when you are multiplying two binomials, you can use a mind trick called FOIL (first, outside, inside, last). Just in case you haven't heard this before, it means multiply the two first terms of each binomial, then the two outside terms, then the two inside terms, and finally, the two last terms. So, for
%28sqrt%28n%2B1%29%2Bsqrt%28n%29%29%28sqrt%28n%2B1%29-sqrt%28n%29%29
So, once we FOIL, we get

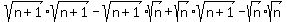
Now, simplifying (remember that sqrt(x)sqrt(x)=x) we get
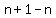
n%2B1-n
1
So, oddly enough, that entire expression simplifies to just 1. Doesn't that just annoy you? :)

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Simplify. Assume that each radical represents a real number.
(√(n+1) +√n)( √(n+1) -√n)
-----------------
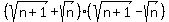
%28sqrt%28n%2B1%29+%2B+sqrt%28n%29%29%2A%28sqrt%28n%2B1%29+-+sqrt%28n%29%29
Treat the radicals as x and y, then it's (x+y)*(x-y) = x^2-y^2
So it's
(n+1) - n
= 1