Question 178041: Conrad has a collection of three types of coins: nickels, dimes and quarters. There are five more nickels than quarters but four times as many dimes as quarters. If the entire collection is worth $5.85, how many nickels, dimes, and quarters are there?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Conrad has a collection of three types of coins: nickels, dimes and quarters.
There are five more nickels than quarters but four times as many dimes as
quarters. If the entire collection is worth $5.85, how many nickels, dimes,
and quarters are there?
:
let n, d, and q = no. of each coin
:
Write an equation for each statement:
:"
" There are five more nickels than quarters"
n = (q+5)
:
" but four times as many dimes as quarters."
d = 4q
:
" If the entire collection is worth $5.85, "
.05n + .10d + .25q = 5.85
:
how many nickels, dimes, and quarters are there?
:
Using the first two equations, substitute for n and d in the total$ equation:
.05(q+5) + .10(4q) + .25q = 5.85
:
.05q + .25 + .4q + .25q = 5.85
:
.05q + .4q + .25q = 5.85 - .25
:
.7q = 5.60
q = 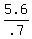
q = 8 quarters
:
I'll let you find the number of nickels and dimes
Check your solutions in the total$ equation
|
|
|