Question 177422: It took Emily 25 min to ride her bike to the repair shop and 1h 15 min to walk back home. If she can ride her bike 8km/h faster than she can walk, how far is the repair shop from her house.
Found 2 solutions by stanbon, Electrified_Levi:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! It took Emily 25 min to ride her bike to the repair shop and 1h 15 min to walk back home. If she can ride her bike 8km/h faster than she can walk, how far is the repair shop from her house.
----------------------
Riding DATA:
time = 25/60 = 5/12 hr ; rate = (r+8)km/h ; distance = rt = (5/12)(r+8) km
------------------------------------
Walking DATA:
time = 5/4 hr ; rate = r km/h ; distance = rt = (5/4)r km
--------------------------------------
Equation:
ride distance = walk distance
(5/12)(r+8) = (5/4)r
(1/12)(r+8) = (1/4)r
r+8 = 3
2r = 8
r = 4 km/h
---------------
walking distance = (5/4)r = (5/4)4 = 5 km
============================================
Cheers,
Stan H.
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
It took Emily 25 min to ride her bike to the repair shop and 1h 15 min to walk back home. If she can ride her bike 8km/h faster than she can walk, how far is the repair shop from her house.
.
To find the answer we need to know a formula
.

.
We can also say  , Emily went on her bike for a distance, and she went back to her home, the same distance , Emily went on her bike for a distance, and she went back to her home, the same distance
.
We don't know how fast it takes Emily to walk, so we will say she walks "x" km/h
.
She can ride her bike 8 km/h fast than she can walk, so she goes " x + 8 " km/h on her bike
.
It takes 25 minutes or 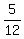 hour ( it has to be the same measurement as the rate ) to ride her bike to the repair shop hour ( it has to be the same measurement as the rate ) to ride her bike to the repair shop
.
It takes her 1hour 15 minutes, or 1 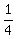 hour to walk back home hour to walk back home
.
The rate of her on the bike multiplied by the time it takes on the bike will equal the rate of her walking multiplied by the time it takes her to walk
.
 = = 
.
Now replace all the unknowns with what we know
.
rate on bike = (x + 8) km/hr
.
time on bike = 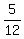 hour hour
.
rate walking = x km/hr
.
time walking = 1 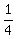 hours or hours or 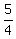 hours hours
.
 = = 
.
 , now we will multiply the numbers out , now we will multiply the numbers out
.
 = =  = =  , we will rearrange the left side , we will rearrange the left side
.
 = =  = = 
.
 , we will use the distribution method to multiply the left side out , we will use the distribution method to multiply the left side out
.
 = =  = =  = =  = = 
.
 , to get rid of the fractions we will multiply each side by "12" , to get rid of the fractions we will multiply each side by "12"
.
 = =  = =

.
Now we will use distribution
.
 = =  = =  = =  = =  , now we will move "5x" to the right side , now we will move "5x" to the right side
.
 = =  = =  = = 
.
to find "x" we will divide each side by "10"
.
 = =  = =  = = 
.
We found "x"
.
We can check by replacing "x" with "4" in our original equation
.
 = =  = = 
.
The denominators cross out
.
 = =  (True) (True)
.
rate walking = x km/hr, we can replace "x" with "4"
.
rate walking = 4 km/hr
.
rate on bike = (x + 8) km/hr, replace "x" with "4"
.
rate on bike = (4 + 8) km/hr
.
rate on bike = 12 km/hr
.
+
+
+
.
rate on bike = 12 km/hr
.
time on bike = 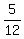 hour hour
.
rate walking = 4 km/hr
.
time walking = 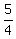 hours hours
.
We can now solve for our answer, since 
.
 = = 
.
The denominators cross out
.
 = = 
.
This means that the distance is 5 km, (since that is the measurement)
.
Your answer is 5 km
.
Hope I helped, Levi
|
|
|