Question 177344: Solve this system of equations
3x+4y+z=7
2y+z=3
-5x+3y+8z=-31
Answer by Electrified_Levi(103)   (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
Solve this system of equations
.
.
This system is a little easier than what we would have to do, but is the same concept
.
We need to solve for one letter in one of the equations, doesn't matter which one, or which equation, we will solve for "z" in the second equation, since it will be the easiest
.
 , to solve "z", we will move "2y" to the right side
.
=  =  or 
.
.
Now that we found "z", we can replace "z" with 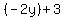 in the other two equations
.
.
replace "z" with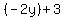
.
 =  , now just combine like terms
.
=  =  =  , now we will move "3" to the right side
.
=  = 
.
is our first answer
.
Now lets replace "z" in the other equation
.
replace "z" with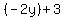
.
 =  , once again just combine like terms, we will use the distributive property to solve even more
.
=  =  , remember the negative/positive signs
.
 =  = 
.
now we will move "24" to the right side
.
=  = 
.
We will make everything positive by multiplying each side by (-1)
.
=  , we will use the distribution method
.
=  =  , remember the signs
.
 = 
.
is our second answer
.
We will now put these two answers into a system
.
.
To make it easier, we will avoid fractions as much as possible
.
We will multiply the first equation by "5"
.
=  =  , using distribution
.
=  =  ,remember signs, = 
.
is the new equation
.
Now we will multiply the second equation by "3"
.
 =  =  , using distribution
.
=  =  , remembering signs, = 
.
is the new equation
.
We will put the two new equations in the system
.
.
We will now use elimination to find "y", we will subtract the bottom equation from the top equation
.
-  , the negative sign makes all the numbers negative
.
Now we need to add the equations
.
________________
.
=  , to find "y" we will divide each side by "29"
.
=  =  = 
.
.
Now replace "y" with "5" in one of the original 2 system equations
.
.
we will use the first equation
.
replace "y" with "5"
.
 =  = 
.
Now we will move "10" to the rights side
.
=  = 
.
To find "x" we can divide each side by "3"
.
=  =  = 
.
.
.
We can check our two answers by replacing "x" and "y" with the numbers in the other 2 system equation
.
=  =  =  ( True )
.
Now all we need to do is find "z"
.
We need to use one of the three original equations
.
.
We will use the second equation
.
.
.
Replace the letters
.
 =  =  , we will move "10" to the right side
.
=  =
.
.
We can check our answers by replacing "x","y", and "z" in the other two equations
.
.
.
.
.
=  =  =  (True)
.
 =  =  =  ( True )
.
These answers are given in the ordered pair ( x,y,z ), our ordered pair/answer is (-2 , 5 , -7 )
.
Hope I helped, Levi
|
|
|
