|
Question 177288This question is from textbook Glencoe Algebra 1
: I am trying to help my son with the following problem regarding solving compound inequalities: 5/x + 3 > 0. I understand the steps involved and how to graph the equation. I can get as far as 5/x > -3 but I don't know how to solve for x or get x on the side by itself.
Thank you for your help
This question is from textbook Glencoe Algebra 1
Found 2 solutions by stanbon, nerdybill:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! solving compound inequalities: 5/x + 3 > 0
----
Notice that x cannot be zero:.
Notice the solution of the EQUALITY goes as follows:
(5/x)+3 = 0
5/x = -3
x = 5/-3
x = -1.666666...
That is the boundary of the inequality
---------------------------------------
Draw a number line and mark x = 0 and x = -1.666666,,,,
-----------------------------------------
Test values in the three resulting intervals
to see where the solutions lie.
-------
Test x = -1/2
[5/(-1/2)] + 3 > 0
-10 + 3 > 0
False
-----------------------------
Test x = -2
[5/-2]+3 > 0
-2.5+3 >0
1/2 >0
True so solutions in -1.6666 < x < 0
-------------------------------
Test x = 1/2
[5/(1/2)] + i3 > 0
10 = 3 > 0
True so solutions in (0,+inf)
-----------------------------
Solution: (-inf,-1.666)U(0,+inf)
==================================
This is what the graph of the EQUALIty looks like:
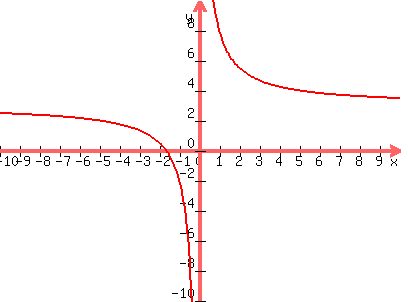
==================================
Cheers,
Stan H.
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! 5/x + 3 > 0
5/x > -3
Multiply both sides by x:
x(5/x) > x(-3)
5 > -3x
Finally, divide both sides by -3:
-5/3 < x
Read 'x' is greater than -5/3
.
Notice that the "greater than" symbol is now reversed as a "less than" symbol -- this is because we divided by a negative number.
|
|
|
| |