Question 177236: factor completely 2x^2 – 128
find all positive and negative intergers b for which the polynomial can be factored.
2x^2 + bx – 15
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 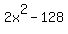 Start with the given expression Start with the given expression
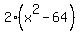 Factor out the GCF Factor out the GCF 
 Factor Factor 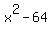 to get to get  (use the difference of squares formula) (use the difference of squares formula)
So 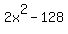 completely factors to completely factors to 
In other words, 
First, take the leading coefficient 2 and the last term -15 and multiply the two numbers to get 
If we want this to be factorable, we need to ask the question: what two numbers multiply to -30 and add to the middle coefficient "b"?
So let's list the factors of  : :
1,2,3,5,6,10,15,30
-1,-2,-3,-5,-6,-10,-15,-30
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to  . .
1*(-30)
2*(-15)
3*(-10)
5*(-6)
(-1)*(30)
(-2)*(15)
(-3)*(10)
(-5)*(6)
Now add them up. The last column represents all of the possible values of "b" that will make 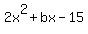 factorable. factorable.
| First Number | Second Number | Sum | | 1 | -30 | 1+(-30)=-29 | | 2 | -15 | 2+(-15)=-13 | | 3 | -10 | 3+(-10)=-7 | | 5 | -6 | 5+(-6)=-1 | | -1 | 30 | -1+30=29 | | -2 | 15 | -2+15=13 | | -3 | 10 | -3+10=7 | | -5 | 6 | -5+6=1 |
=====================================================
Answer:
So the possible values of "b" are: -29, -13, -7, -1, 29, 13, 7, and 1 (look at the third column of the table above)
|
|
|