Question 177100This question is from textbook Blitzer College Algebra
: If a rock is thrown upward with an initial velocity of 32 feet per second from the top of a 40-story building,write the height equation using this information.
How high is the rock after 0.5 seconds? How many seconds will the rock reach maximum height? What is the maximum height?
This question is from textbook Blitzer College Algebra
Found 3 solutions by jim_thompson5910, amalm06, Alan3354:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! "write the height equation using this information"
Remember, the general height equation is  where "s" is the position of the object, "t" is the time, where "s" is the position of the object, "t" is the time,  is the initial velocity, and is the initial velocity, and 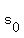 is the initial position. is the initial position.
Since the "initial velocity of 32 feet per secound from the top of a 40 foot building", this means that  and and 
So the equation is  (after plugging in the initial velocity and position) (after plugging in the initial velocity and position)
--------------------------------------------------
b)
"how high is the rock after 5.0 seconds?"
Are you sure that the "5" isn't "0.5"? After 5 seconds, the rock wouldn't be in the air.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square 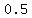 to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Multiply Multiply  and and 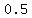 to get to get  . .
 Combine like terms. Combine like terms.
So after 0.5 seconds (half a second), the object is 52 ft in the air.
--------------------------------------------------------------------
c)
"after how many seconds will the rock reach maximum height"
To find the time where the object reaches the max height, we need to find the x-coordinate vertex of 
 Start with the vertex formula. Start with the vertex formula.
From  , we can see that , we can see that  , ,  , and , and  . .
 Plug in Plug in  and and  . .
 Multiply 2 and Multiply 2 and  to get to get 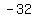 . .
 Divide. Divide.
So at one second, the object will reach the max height.
-----------------------------------------------------------------
d)
"what is the maximum height?"
 Start with the given equation. Start with the given equation.
 Plug in Plug in  (the time at which the object will reach the peak). (the time at which the object will reach the peak).
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Combine like terms. Combine like terms.
So the max height is 56 feet.
Answer by amalm06(224)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem can be solved using momentum and energy considerations. The net force acting on the rock causes the velocity of the rock to change. This is given by the following impulse-momentum equation:
FΔt=m(vf-v0)
Since gravity is the only force that acts on the rock:
mgΔt=m(vf-v0)
gΔt=vf-v0, where g=-32 ft/s^2.
Then (-32)(Δt)=vf-v0
At maximum height, the velocity of the rock is zero. If you imagine the trajectory of the rock to follow a symmetrical parabolic path, then the slope of the horizontal tangent is zero at maximum height. But this slope is just the first derivative of the position, which is the velocity.
Then (-32)((Δt)=0-32 = -32
Therefore, t=1. The rock reaches maximum height after 1 second (Answer).
At maximum height, the rock has only potential energy. Since we are neglecting air resistance, friction does no work on the rock:
(1/2)(m)(V^2)i=mg(h2-40)
0.5(v^2)i=g(h2-40)
(0.5)(32)=(32)(h2-40)
16=h2-40
h2=56 ft. The maximum height of the rock is 56 ft (Answer)
To find the height of the rock after 0.5 seconds, use the following formula:
Δy=Vit + 0.5a(t^2)
So that y2-40=32t+(0.5)(-32)(t^2)
y2=32t-16(t^2)+40
y2=-16(t^2)+32t+40
For t=0.5 seconds, y2=-4+16+40=52 ft (Answer)
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a rock is thrown upward with an initial velocity of 32 feet per second from the top of a 40-story building,write the height equation using this information.
How high is the rock after 0.5 seconds? How many seconds will the rock reach maximum height? What is the maximum height?
==============
What's the height of 40 stories?
----
Using 400 ft for the 40 stories:
h(t) = -16t^2 + 32t + 400 --- h in feet, t in seconds
----
How high is the rock after 0.5 seconds?
h(0.5) = -16*(0.25) + 32*0.5 + 400 = 412 feet
----
How many seconds will the rock reach maximum height?
That's the vertex of the parabola at t = -b/2a
t = -32/-32 = 1 second.
-----
What is the maximum height?
h(1) = -16 + 32 + 400 = 416 feet.
|
|
|