|
Question 176999: Find the domain and range of this function f(x)=1/squareroot of (x-4)
Found 2 solutions by Fombitz, rapaljer:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! The domain is all of the x values that make f(x) defined.
There are two restrictions on the domain to be concerned about.
First, the square root can only have zero or positive values as arguments, because the square root of a negative number is undefined.

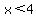
Second, since it's a fraction, the denominator cannot be zero because division by zero is undefined.
Find the point(s) where the denominator equals zero.


If we put the two together, x cannot be less than 4 and x cannot be equal to 4.
Therefore the domain is x such that x is greater than 4.
Domain:( , , ) )
.
.
.
To get the range look at the domain.
Near x gets close to 4 (say 4.001), the denominator gets very small, the value of f(x) gets zero large.
As x gets very larger, the denominator gets very large, the value of f(x) goes towards 0.
Range:( , , ) )
Answer by rapaljer(4671)   (Show Source): (Show Source):
You can put this solution on YOUR website! DOMAIN:
Domain is the set of all permissible x values. Since there is a square root in a denominator, the denominator can't equal 0, and the radicand cannot be negative. Therefore x-4>0, so x>4.
RANGE:
Since  there is a built-in restriction that f(x) cannot be negative or zero, since it's value is determined by the there is a built-in restriction that f(x) cannot be negative or zero, since it's value is determined by the  . Moreover, as x gets closer and closer to 4, the value of f(x) gets larger and larger, approaching infinity. . Moreover, as x gets closer and closer to 4, the value of f(x) gets larger and larger, approaching infinity.
Final answer in interval notation:
D: x>4 (4,inf)
R: y>0 (0, inf)
R^2
|
|
|
| |