Question 176743: In a family there are two cars. The sum of the average miles per gallon obtained by the two cars in a particular week is 50 . The first car has consumed 30 gallons during that week, and the second has consumed 20 gallons, for a total of 1300 miles driven by the two cars combined. What was the average gas mileage obtained by each of the two cars in that week?
Found 2 solutions by Mathtut, MathTherapy:
Answer by Mathtut(3670)   (Show Source):
You can put this solution on YOUR website! let x and y be the avg gas mileage of car 1 and car 2 respectively
:
x+y=50...........eq 1
30x+20y=1300.....eq 2
:
rewrite eq 1 to x=50-y and plug in the value to eq 2
:
30(50-y)+20y=1300
:
1500-30y+20y=1300
:
-10y=-200
:
 mpg car 2
:
x=50-y mpg car 1
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website! Let the amount of miles that the car that consumed 30 gallons of gas went, be x
Then the amount of miles that the car that consumed 20 gallons of gas went, is 1,300 – x
Then,  + =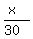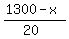
2x + 3(1,300 - x) = 3,000
2x + 3,900 - 3x = 3,000
x = 900
Since the car that consumed 30 gallons of gas went 900 miles that week, then the average gas mileage it got was 900 ÷ 30 = 30 miles per gallon
Since the car that consumed 20 gallons of gas went 1,300 – 900, or 400 miles that same week, then the average gas mileage it got was 400 ÷ 20 = 20 miles per gallon
|
|
|
