Question 175901This question is from textbook algebra 1
: Gerry and Tony live 11km apart. Gerry leaves his home at 2 p.m. and bikes toward Tony's home at 25 km/hr. At the same time, Tony leaves his home and bikes toward Gerry's home at 30 km/hr as soon as they reach each other's homes they turn around and start back along the same route. They stop when they meet each other on the ride back to their own homes. How far are they are from Gerry's home when they stop?
This question is from textbook algebra 1
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! For both,

Each has their own rates, times and distances, so
 Tony's equation Tony's equation
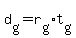 Gerry's equation Gerry's equation
Each bikes to the others house and they leave at the same time, so
For Tony,

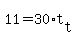
 hrs hrs
and, for Gerry,
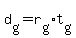

 hr hr
Comparing these, with LCD


So, Tony got to Gerry's house 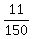 hrs quicker hrs quicker
than Gerry got to Tony's house.
-------------------
Now, they turn around and head back toward eachother.
If they left at the exact same time, the elapsed
time for each until they met would be the same
 , but Tony gets a head start. , but Tony gets a head start.
-------------------
Assume I have a stopwatch and I'm in a helicopter overhead
so I can see both of them. I'll start the stopwatch when
Gerry turns around 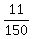 hr after Tony has turned around. hr after Tony has turned around.
If Gerry's time to where they meet from Tony's house is 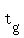
then Tony's time from Gerry's house is 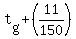
--------------------
Now my equations are
 km km

where these are the distances each travel to where they meet
(1) 
(2) 
rewriting (1)
(1) 
Substitute (2) in (1)



 hr hr
 hrs or hrs or  min min
------------------
The distance Tony travels is the distance from Gerry's
house when they meet
(1) 


 km km
They meet 7 km from Gerry's house
check answer:
(2) 
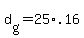

and
 km km

OK
|
|
|