Question 175889: Hello, I'm having trouble understanding this question. I'm not very sure what it's asking me, and thus I'm not sure where I should begin. Any help would be much appreciated!
Use absolute value and the variable "x" to write an open sentence that specifies the numbers on a number line whose distance from (3/2) is less than (5/2).
Answer by EMStelley(208)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's first talk about what distance means. If I asked you the distance between 10 and 1 on the number line, how would you find that? You would subtract 1 from 10, resulting in 9. We want to use the same idea here. The distance between x and 3/2 can be represented by x - 3/2. For example, if x is 3, the distance would be 3/2, and if x is -1, the distance would be 5/2 (absolute value of -5/2 since distance is never negative). So the distance between x and 3/2 can be written as

Now, since we want that distance to be less than 5/2, we literally just tack that on to the end.
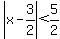
So in order to find the numbers, x, that really are less than 5/2 away from 3/2, you need to solve that absolute value inequality. Is this enough? I hope so.
|
|
|