Question 175629This question is from textbook Algebra 1
: If the digits of a two-digit positive interger are reversed, the result is 6 less than twice the original numder. Find all such intergers for which this is true.
How do you figure this out?
This question is from textbook Algebra 1
Found 4 solutions by ankor@dixie-net.com, Mathtut, josmiceli, solver91311:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
Answer by Mathtut(3670)   (Show Source): (Show Source):
You can put this solution on YOUR website! lets call our digits a and b written as ab
:
now remember ab can also be written as 10a+b
and when it is reverse it is ba which can be written as 10b+a
:
so with that info lets write the equation: they only gave us enough info for one equation so we are going to have to do some surmising on this one:
:
10b+a=2(10a+b)-6
:
10b+a=20a+2b-6
:
8b-19a=-6
:
the only possibilities for this scenario is digits 0-9 for both a and b. the question is can we find an integer value for both a and b that satisfies this equation.
the value of 19a always has to be more that the value of 8b in order to get -6
:
so for a=1 b can only be 1 or 2 (8-19),(16-19)...neither of which works
a=2 so 19a=38.. so we need 8b=32...8(4)=32 so we have a pair a=2 b=4.
a=3 so 19a=57...so we need 8b=51....no integer value will work
a=4 so 19a=76...so we need 8b=70....no integer value will work
a=5 so 19a=95...so we need 8b=89---> we have exhaused our possibilities here. as you can see in order for 8b=89 we would have to multiply by two digit number and as the value of 19a gets higher the same will hold true
:
so we have found the only integers for which this is true and
:
they are
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the tens digit be represented by 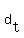 and the ones digit be represented by and the ones digit be represented by 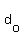 . That means you can represent any two digit positive number by . That means you can represent any two digit positive number by 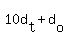 if you restrict if you restrict 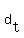 and and 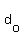 to the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. to the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.
If our original number is 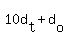 then the number with reversed digits is then the number with reversed digits is 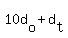 . Then the conditions of the problem give us: . Then the conditions of the problem give us:

Simplify and solve for 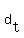



Now remember that both 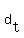 and and 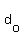 are restricted to the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. That means that we have to find which of the given set of numbers, when substituted for are restricted to the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. That means that we have to find which of the given set of numbers, when substituted for 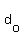 , yield , yield 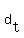 also an element of the given set. We know that since the denominator is 19 and there are only ten consecutive integer possibilities, we have at most 1 solution. also an element of the given set. We know that since the denominator is 19 and there are only ten consecutive integer possibilities, we have at most 1 solution.
We can also see that 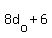 must be an integer multiple of 19. must be an integer multiple of 19.
The first five integer multiples of 19 are 19, 38, 57, 76, and 95. So:
 → →  → → 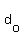 not an integer. not an integer.
 → →  → →  IS an integer. This is our solution, but let's continue just to make sure. IS an integer. This is our solution, but let's continue just to make sure.
 → →  → → 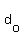 not an integer. not an integer.
 → →  → → 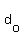 not an integer. not an integer.
 → →  → → 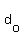 not an integer AND not an integer AND 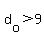 so we can stop looking. so we can stop looking.
Now we know the ones digit is 4, so using  we know the tens digit is 2. we know the tens digit is 2.
The only positive two-digit integer that satisfies the given conditions is 24.
Check the answer:
2 times 24 is 48 which is 6 more than 42 which is 24 with the digits reversed. Checks.
By the way, the word is integer, not interger.
|
|
|