|
Question 175440: times to unload a certain truck:
al,bob,chuck together t hours
al alone t+1
bob alone t+6
chuck alone 2t
find t
Found 4 solutions by stanbon, josmiceli, ptaylor, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! times to unload a certain truck:
al,bob,chuck together t hours
al alone t+1
bob alone t+6
chuck alone 2t
find t
-----------------------
You are given the time for each person and the group.
For example Al alone takes (t+1) hr/job
Invert that to get Al's rate: 1/(t+1) job/hr
------------------------------------------------
Equation:
rate + rate + rate = together rate
1/(t+1) + 1/(t+6) + 1/2t = 1/t
Multiply thru by 2t(t+1)(t+6) to get:
2t(t+6) + 2t(t+1) + (t+1)(t+6) = 2(t+1)(t+6)
2t^2+12t + 2t^2 + 2t + t^2 + 7t + 6 = 2t^2 + 14t + 12
3t^2 + 7t -6 = 0
3t^2 + 9t - 2t-6 = 0
3t(t+3) -2(t+3) = 0
(t+3)(3t-2) = 0
Positive solution:
t = 2/3 hr
=============
Cheers,
Stan H.
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by ptaylor(2198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
al, bob, chuck together work at the rate of 1/t truck per hour
al works at the rate of 1/(t+1) truck per hour
bob works at the rate of 1/(t+6) truck per hour
chuck works at the rate of 1/(2t) truck per hour
Now we know that:
(1/(t+1))+(1/(t+6))+(1/(2t))=1/t multiply each term by 2t(t+1)(t+6)
2t(t+6)+2t(t+1)+(t+1)(t+6)=2(t+1)(t+6) get rid of parens
2t^2+12t+2t^2+2t+t^2+7t+6=2t^2+14t+12 simplify
5t^2+21t+6=2t^2+14t+12 subtract 2t^2, 14t and 12 from each side
3t^2+7t-6=0 quadratic in standard form and it can be factored
(3t-2)(t+3)=0
3t-2=0
t=2/3 hr---------------------------answer
and
t+3=0
t=-3 hrs----disregard--time in this case is positive
CK
1/(2/3 +1) + 1/(2/3+6) + 1/(2*2/3)=1/(2/3)
3/5 + 3/20 + 3/4=3/2
12/20 + 3/20 =15/20=3/2
30/20=3/2
2/2=3/2
Does this help??? ------ptaylor
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given A can do the work in x hours and B can do the work in y hours, you proceed by saying A can do  th of the job in 1 hour and B can do th of the job in 1 hour and B can do  th of the job in 1 hour, so together they can do th of the job in 1 hour, so together they can do 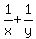 th of the job in 1 hour and therefore can do the whole job in th of the job in 1 hour and therefore can do the whole job in  hours. The above can be extended to as many workers as you like just by adding terms. hours. The above can be extended to as many workers as you like just by adding terms.
So for your problem:
A can do the work in 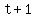 hours, therefore can do hours, therefore can do 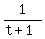 of the job in 1 hour. of the job in 1 hour.
B can do the work in  hours, therefore can do hours, therefore can do 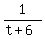 of the job in 1 hour. of the job in 1 hour.
C can do the work in  hours, therefore can do hours, therefore can do  of the job in 1 hour. of the job in 1 hour.
Together they can do the whole job in  hours, so they can do hours, so they can do 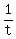 of the job in 1 hour. of the job in 1 hour.
Therefore:
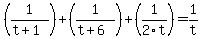
This looks like an algebraic horror, but really isn't that bad. First, find the common denominator. The factors of the common denominator are 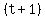 , , 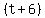 , ,  , and , and  , and only the , and only the  and and  have the common factor have the common factor  , so we can eliminate that making the LCD the product: , so we can eliminate that making the LCD the product: 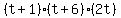 . It will be convenient to leave the LCD in that form as you will see. . It will be convenient to leave the LCD in that form as you will see.
Applying the LCD we get:

The first thing to do to simplify this mess is to multiply both sides of the equation by the denominator leaving the two numerator expressions equal:

Next, perform the indicated multiplications:

Remove the parentheses:

Collect terms on the left:

Add 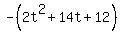 to both sides: to both sides:

Leaving us with a not too unattractive little quadratic to solve. I say not too unattractive because the thing actually factors:

So:  → →  or or  → → 
Notice that  is an absurd answer because that would mean if they started the job now, they would be done three hours ago. What happened is that in the process of solving the problem we squared the variable and that introduced an extraneous root. Exclude is an absurd answer because that would mean if they started the job now, they would be done three hours ago. What happened is that in the process of solving the problem we squared the variable and that introduced an extraneous root. Exclude  , leaving us with , leaving us with  as our solution set. as our solution set.
Check the answer:
A can do the work in 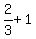 hours, therefore can do hours, therefore can do 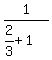 of the job in 1 hour. of the job in 1 hour.
B can do the work in 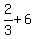 hours, therefore can do hours, therefore can do 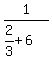 of the job in 1 hour. of the job in 1 hour.
C can do the work in 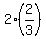 hours, therefore can do hours, therefore can do 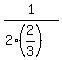 of the job in 1 hour. of the job in 1 hour.
Together they can do the whole job in  hours, so they can do hours, so they can do  of the job in 1 hour. of the job in 1 hour.


 Answer checks. Answer checks.
Super Double Plus Extra Credit
Say that you are paying each of these three guys $15.00 per hour and your customer is paying you $75 to get the truck loaded.
1. What is your profit given the stated conditions?
2. What action could you take to maximize your profit (aside from doing the whole job yourself)? By how much?
|
|
|
| |