Question 175133: Could someone help me understand this problem?
- Find the length and the equation of the median of the triangle ABC from A to BC id A(2,-6), B(-7,4), and C(1,12).
I tried
AB= (square root sign)((-7)-2)^2+(4-(-6))^2 = 13.45
BC= (square root sign) (1-(-7))^2+(12-4)^2 = 11.31
CA= (square root sign) (2-1)^2+((-6)-12)^2 = 18.02
and was marked wrong.
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! the median of the triangle from A to BC intersects line BC at its midpoint.
we'll call that point D.
---
you need to find the midpoint of the line BC and then you need to find the equation of the line AD.
---
the coordinates for the midpoint of a line is ((x1+x2)/2,(y1+y2)/2)
---
line BC is given by the points:
(x1,y1) = (-7,4)
(x2,y2) = (1,12)
---
the midpoint of line BD is:
((-7+1)/2,(4+12)/2)
this equals:
(-3,8)
---
the coordinates for point D are (-3,8) which is the midpoint of line BC.
---
line AD is the median of line BC.
the length of line AD is given by the equation:
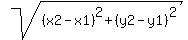
where:
(x1,y1) = (2,-6)
(x2,y2) = (-3,8)
---
this comes out to be:
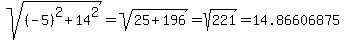
---
the equation for this line would be:
y = m*x + b
m = slope = 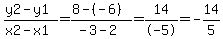
---
take one of the points (either one will do) and substitute in the equation to get the y intercept.
y = m*x + b
m = -14/5
point used = (-3,8)
8 = (-14/5)*(-3) + b
8 = 42/5 + b
8 - 42/5 = b
b = -2/5
equation for the median line AD is:
y = -14/5*x - 2/5
---
in the graph below:
point A (2,-6) is the intersection of 3 lines on the lower right (AB,AD,AC).
point B (-7,4) is the intersection of 2 lines on the middle left (AB,BC).
point C (1,12) is the intersection of 2 lines on the upper right (AC,BC).
point D (-3,8) is the intersection of 2 lines in between points B and C (AD,BC).
---
if you print the graph and label them, it should be easier to see.
---

|
|
|