SOLUTION: can you please help me solve: 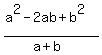{{{(a^2-2ab+b^2)/(a+b)}}}

That is not an equation or an inequality, so it can't be
"solved".  It is an expression, and expressions cannot be
said to be "solved" but only "simplified" or "rewritten".
Only equations and equalities can be said to be "solved".     

To try to simplify it, we first try factoring the top:





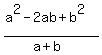
or



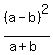But nothing cancels because we have - between a and b on
top and + between a and b on the bottom.  Are you sure you
typed all the signs right?

As you have it, it may be divided out by long division:

              a -  3b 
      ----------------
a + b )a2 - 2ab +  b2
       a2 +  ab
       --------
           -3ab +  b2
           -3ab - 3b2
           ----------
                  4b2

Then the expression may be rewritten as 

Or, you could rearrange the terms in descending order
of b instead of a, and get:

              b -  3a 
      ----------------
b + a )b2 - 2ab +  a2
       b2 +  ba
       --------
           -3ba +  a2
           -3ba - 3a2
           ----------
                  4a2

Then the expression can also be rewritten as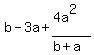 

So you can rewrite, not "solve", 



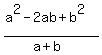as either

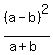, , or 

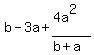but expressions can only be simplified or rewritten.

Only equations and inequalities can be solved. 

Edwin