Question 174973: I need help!!
- A car travelled 470 km from Sudbury to Brandford in 5 hours. For part of the trip, the car travelled at 100 km/h. For the rest of the trip, it travelled at 90 km/h. How far did the car travel at each speed?
I tried
x+y=5
100x+90=470
100x+100y=500
100x+90y=470
= 10y = 30
x=2 y=3
but I only got half marks. Where did I go wrong and what was the answer?
Found 2 solutions by Electrified_Levi, stanbon:
Answer by Electrified_Levi(103)   (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
I need help!!
- A car travelled 470 km from Sudbury to Brandford in 5 hours. For part of the trip, the car travelled at 100 km/h. For the rest of the trip, it travelled at 90 km/h. How far did the car travel at each speed?
.
We will start fresh
.
First we need to know a formula
.
 , or with abbreviations, 
.
A car travelled 470 km from Sudbury to Brandford in 5 hours. For part of the trip, the car travelled at 100 km/h. For the rest of the trip, it travelled at 90 km/h. How far did the car travel at each speed?
.
This problem is a little tricky, since the car is going two speeds, instead of just one, we also have two different times.
.
This will mean we will have two unknowns, we can find the other unknowns with the information we have
.
A car travelled 470 km from Sudbury to Brandford in 5 hours. For part of the trip, the car travelled at 100 km/h. For the rest of the trip, it travelled at 90 km/h. How far did the car travel at each speed?
.
Remember that  , we don't know the time or distance for either one of the speeds, but we know the total distance and total time
.
We can say that the time it took when the car went 90 km/h, the time it took would be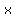 
.
We can say that how long it took when the car went 100 km/h, the time it took would be 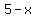 , ( if you subtract the other time, from the total time, you will find the second unknown time )
.
It is the same concept with the distances
.
one distance would be 
.
the second unknown distance would be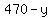 
.
We can now find equations to this problem
.
.
Equation 1
.
if the car went 100 km/h ( rate )
.
if the car took 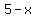hours ( time ), ( doesn't matter which time we could use "x" if we wanted, but we will use this one )
.
These two multiplied together will equal a distance 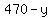, ( once again it doen't matter which distance, we could use "y" if we wanted )
.
Now we would put the words into a formula,
.
 =  , this is the first equation
.
Now we will use the other distance, time, and rate, to find the second equation
.
If the car went 90 km/h ( rate )
.
If the car took hours ( time )
.
If the car drove km ( distance )
.
Now replace "r", "t" and "d" with the other veriables
.
=  , this is the second equation
.
Now we can put these two equations side by side
.
.
To make it easier, we will simplify the two equations
.
Equation 1, , we can use the distribution to simplify this equation
.
=  = 
(remember the signs
.
 =  , we don't have to move anything right now, so this is the simplified form
.
Equation 2, we will just multiply the "90" and "x"
.
=  , this is simplified
.
Now we can start solving for the two unknowns
.
.
This is a system of equations, the easiest way to solve this system is by substitution
.
Since  , we can just simply replace "y" in the first equation with "90x"
.
= 
.
=  , now we can just solve for "x", we will move (-100x) to the right side
.
=  =  , now we will move "470" to the left side
.
=  =  , to find "x" we will divide each side by "10"
.
=  =  =  =  , 
.
(remember "x" is the time in hours), we can replace "x" with "3" in the second equation, to find "y"
.
=  =  ,  , we can check our two answers by replacing "x" and "y" in the first equation
.
x = 3
.
y = 270
.
=  =  =  (True)
.
Here are the simplified equations with the numbers
.
.
.
If we look at the formula,
.
.
This means that the car went 200 km at 100 km/h, and it went 100 km/h for 2 hours
.
The car went 270 km at 90 km/h, and it went 90 km/h for 3 hours
.
The distances add up to the total distance, as well as the time with the total time
.
The car went 200 km at 100 km/h
.
The car went 270 km at 90 km/h
.
Hope I helped, Levi
Answer by stanbon(75887) (Show Source):
You can put this solution on YOUR website! A car travelled 470 km from Sudbury to Brandford in 5 hours. For part of the trip, the car traveled at 100 km/h. For the rest of the trip it traveled at 90 km/h. How far did the car travel at each speed?
--------------------------
100 kph section DATA:
Distance = x km ; rate = 100 kph ; time = d/r = x/100 hrs.
--------------------
90 kph section DATA:
Distance = 470 - x km ; rate = 90 kph ; time = d/r = (470-x)/90 hrs
==========================
EQUATION:
time + time = 5 hrs
x/100 + (470-x)/90 = 5
90x + 100(470-x) = 450*100
90x + 100*470 - 100x = 450*100
-10x = -20*100
x = 200 km (distance traveled at 100 kph)
470-x = 270 km (distance traveled at 90 kph)
================================================
Cheers,
Stan H.
|
|
|
