Which of the following sets is closed under division?
a. nonzero whole numbers
No, it's not closed because it's possible to divide our
way out of the set of whole numbers. For example we can
start with two nonzero whole numbers, say 5 and 2, and
divide them and get 2.5, which is NOT a whole number.
So we have divided our way out of the set of whole
numbers. Since this is possible, the set of
nonzero whole numbers is not closed under division.
b. nonzero integers
No, it's not closed, for non-zero whole numbers are
nonzero integers, and the above example shows that
it's not closed.
c. nonzero even integers
No because it's possible to divide our way out of the set of
nonzero even integers. For example we can start with two nonzero
even integers, say 8 and 6, and divide them and get 
, which
is NOT a nonzero even integer. So we have divided our way out of the
set of nonzero even integers. Since this is possible, the set of
nonzero even integers is not closed under division.
d. nonzero rational numbers
Yes because it is impossible to divide our way out of the set of
nonzero rational numbers. For example we can start with two nonzero
rational numbers, say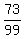 
and 
, which is indeed a nonzero rational number. So we cannot
divide our way out of the set of nonzero rational numbers. Since this
is not possible, the set of nonzero rational numbers is indeed closed
under division.
Edwin
(