SOLUTION: I been working on these problems with my daugther but not very good. Question one. Graph the inequality on a plane 8x-7 less than 15x+y. Second problem Graph the system of inequal

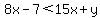First draw the graph of the boundary line, which has
the equation formed by replacing the inequality
symbol <  by =. So first graph  by 
finding two points.  

let, say, x=0, substitute in  



So one point on that line is 

Now let, say, y=0, substitute in  



So another point on that line is 
So we plot those two points, and draw a dotted line through
them:



Now we have to shade one side of that line.  So we choose
any point that is NOT on that line to see if it is or is not
a solution to the original inequality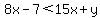 

Let's arbitrarily pick a test point, say (3,2), and substitute
x=3 and y=2 in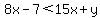 






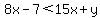
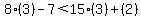
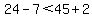
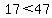Since that is true, we have chosen
a point on the side of the line where
ALL the solutions lie, so all the solutions
to the inequality lie on the same side of
the line as (3,2). So we shade that side of
the line.  I can't shade on here, but you
can on your paper:





Second problem  Graph the system of inequalities. 
system.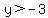 

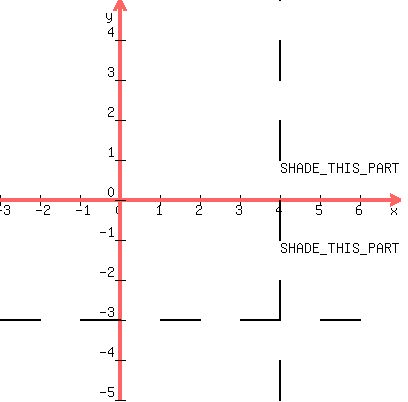
Draw the graph of  which is a dotted horizontal line.
Draw the graph of  which is a dotted vertical line.

Since the inequality is , its solution is ABOVE
this horizontal line.

Since the first inequality is , its solution is TO
THE RIGHT OF this horizontal line.

So only shade the area which is ABOVE the horizontal line
and TO THE RIGHT OF the vertical line.

The last two inequalities are the areas above the x-axis
and to the right of the y-axis. Their boundaries are the
axes themselves.  You'll shade the the part that is below
each of the dotted lines and to the right of the axes:


Edwin