Question 174494: Quadrilateral ABCD has vertices A(-1,0), B(3,3), C(6,-1), and D(2,-4). Prove that quadrilateral ABCD is a square.
Found 2 solutions by checkley77, jojo14344:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! A(-1,0), B(3,3), C(6,-1), D(2,-4).
slopes:
AB=(3-0)/(3+1)=3/4
DC=(-4+1)/(2-6)=3/4 THUS THESE 2 LINES ARE PARALLEL.
slopes:
BC=(-1-3)/6-3)=-4/3=-4/3
AD=(-4-0)/(2+1)=-4/3 THESE 2 LINES ARE PARALLEL & PERPENDICULAR TO THE AB & DC LINES.
THUS THIS IS A SQUARE FIGURE.
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website!
ABCD has vertices A(-1,0), B(3,3), C(6,-1), and D(2,-4)
Let's see 3 important properties of a Square:
1) All sides are EQUAL.
2) The Diagonals are equal.3
3) Each Angle is equal to 90 degress.
.
To Prove the properties, let's draw the Square first with given vertices:

1) All SIDES ARE EQUAL.
To prove, we use distance Formula ---->
For  : :


For  : :


For  : :


For 


.
Therefore, you can see all SIDES are EQUAL IN LENGTH,
It follows, as you see in the graph:

.
2) The Diagonals are EQUAL.
The diagonals here are referred to  adn adn  . And again we use Distance formula, . And again we use Distance formula, 
For  : :


For  ; ;


Therefore: 
It satisfy the 2nd property, and as we see in the graph:

.
3) Each Angle is equal to 90 DEGREES
In this property we use Equation for Right Traingles, the Pythagorean theorem.
Just where the formula we used above is derived from.
For Triangle  : :



 , A Right Triangle! , A Right Triangle!
For Triangle  : :


 , A Right Triangle! , A Right Triangle!
For Triangle 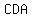


 , A Right Triangle , A Right Triangle
For Triangle 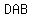


 , A Right Triangle! , A Right Triangle!
ALL satisfies the Pythagorean theorem, therefore all angles are 90 degrees:
.
Conclusion: ABCD that has vertices A(-1,0), B(3,3), C(6,-1), and D(2,-4) is a SQUARE.
Thank you,
Jojo
|
|
|