Question 174362: Find an equation of the line that is parallel to the line y=-4/3x+7 and that passes through the point (7,3).
Found 4 solutions by nerdybill, Mathtut, Alan3354, Electrified_Levi:
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an equation of the line that is parallel to the line
If a line is to be parallel to:
y=-4/3x+7
It must have the same slope: -4/3
That, along with the given point of (7,3) is plugged into the "point-slope" form:
y-y1 = m(x-x1)
y-3 = (-4/3)(x-7)
y-3 = (-4/3)(x)- 7(-4/3)
y-3 = (-4/3)(x)+ 28/3
y = (-4/3)(x)+ 28/3 +3
y = (-4/3)(x)+ 28/3 + 9/3
y = (-4/3)(x)+ 37/3 (this is what you're looking for)
Answer by Mathtut(3670)   (Show Source): (Show Source):
You can put this solution on YOUR website! lines that are parallel have equal slopes so the slope of the line we are looking for has a slope of -4/3
:
using the point slope formula
:
y-3=-4/3(x-7)
:
y-3=-4/3(x)+28/3......multiply terms by 3
:
3y-9=-4x+28
:

Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an equation of the line that is parallel to the line y=-4/3x+7 and that passes through the point (7,3).
-----------
It's not "an equation", it's the equation. There's only one.
y=-4/3x+7
The slope is -4/3, as the eqn is in the slope-intercept form.
Any line parallel to it will have the same slope.
So,
y-y1 = m*(x-x1) (m is the slope)
y-3 = (-4/3)*(x-7)
3y-9 = -4*(x-7)
3y-0 = -4x+28
4x+3y = 28
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Find an equation of the line that is parallel to the line  and that passes through the point (7,3) and that passes through the point (7,3)
.
We are trying to find a line parallel to this line
.

.
lines are given in the form  , where "m" is the slope, and "b" is the y intercept , where "m" is the slope, and "b" is the y intercept
.
 , this line has a slope of , this line has a slope of 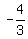 , and y intercept of "7" , and y intercept of "7"
.
We are trying to find a parallel line, so that means the line will have the same slope as the other, or 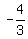
.
If we took the line form  , we can start replacing the letters for our unknown line , we can start replacing the letters for our unknown line
.
We know that "m" is 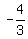 , since it is parallel to the given line , since it is parallel to the given line
.
Our new formula is
.
 ( we replaced "m" with the known slope ( we replaced "m" with the known slope 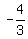 ) )
.
 , we now have 3 variables, we will have to get rid of 2 of them , we now have 3 variables, we will have to get rid of 2 of them
.
We are also given a point, (7,3)
.
Points are in the form of (x,y)
.
(7,3):(x,y)
.
x = 7
.
y = 3
.
 , now replace the "x" and "y" with the numbers , now replace the "x" and "y" with the numbers
.
 = =  = = 
.
Now we just need to solve for "b"
.
 , we will move the , we will move the 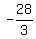 over to the left side over to the left side
.
 = =  = =  = =  = =  , or , or 
.
You can check your answer by replacing "b" with 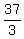 in the equation in the equation
.
 = =  = =  = =  (True) (True)
.
Now just replace "b" in our original equation ( one where we had "x" and "y" )
.
 = = 
.
 is the line in point slope form, if you want it in standard form is the line in point slope form, if you want it in standard form  , here is how you would convert it , here is how you would convert it
.
 , you would first multiply each side by "3" , you would first multiply each side by "3"
.
 = =  , using distribution , using distribution
.
 = =  = = 
.
 = = 
.
Now we need to move (-4x) to the left side
.
 = =  = = 
.
Rearranging the left side
.
 = =  , this is the standard form of the equation , this is the standard form of the equation
.
If you want to see if a point is on a line you would replace "x" and "y" with the point (x,y)
.
Our point is (7,3)(x,y)
.
x = 7
.
y = 3
.
 = =  = =  = =  (True) (True)
.
The graph of this line is
.

.
It is parallel to the original line and has (7,3) as a point
.

.
Your line that you were looking for or your answer is
.
Standard form: 
.
Point-Slope form: 
.
Hope I helped, Levi
|
|
|