|
Question 174317: Find the equation of the line that passes through the point (4, -1) and is perpendicular to: 3X-5Y-2
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! I can only guess at the equation of the given line because you didn't state it as an equation, however both likely possibilities result in the same equation, so I'm going to assume you meant:
Step 1 is to solve your equation for  , that is, add 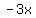 to both sides, then multiply both sides by  . The resulting coefficient on x will be the slope of the given line.
Step 2: Parallel lines have equal slopes, so to find the equation of a parallel line, you need to find the equation that passes through the given point ( , ) = (4, -1) with the same slope as the given line. We'll just call that slope  for this discussion, but you will replace with the slope value you determined in Step 1. Knowing the slope and a point, you can determine the equation of a line using the point-slope form of a line:
 .
Just substitute the calculated value for and the given coordinates for and , and simplify. Since your given line was presented in standard form  and the desired form for your answer is not specified, your answer should be presented in standard form as well.
|
|
|
| |
