SOLUTION: Using the LCD to simplify Complex Fractions. This problem has me stumped, can you help ? 4ab^5 ------ a+b ----- 6a^2b^4 I think the LCD for this one is 1/6a^2b^4. Please

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Using the LCD to simplify Complex Fractions. This problem has me stumped, can you help ? 4ab^5 ------ a+b ----- 6a^2b^4 I think the LCD for this one is 1/6a^2b^4. Please       Log On


   

Question 174308This question is from textbook Elementary and Intermediate Algebra
: Using the LCD to simplify Complex Fractions. This problem has me stumped, can you help ?
4ab^5
------
a+b
-----
6a^2b^4
I think the LCD for this one is 1/6a^2b^4. Please show me the steps This question is from textbook Elementary and Intermediate Algebra

Found 2 solutions by Earlsdon, solver91311:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Simplify:
%28%284ab%5E5%29%2F%28a%2Bb%29%29%2F%286a%5E2b%5E4%29 To divide fractions, you "copy-flip-flip" That is: Copy the first fraction, flip the sign from divide to multiply, flip (invert) the second fraction.
%28%284a%2Ab%5E5%29%2F%28%28a%2Bb%29%29%29%2A%281%2F6a%5E2b%5E4%29 Rewrite this after some factoring.
Cancel the indicated factors to get:
2b%2F%283a%28a%2Bb%29%29

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
I think you are trying to illustrate the following:

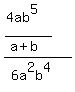
%28%284ab%5E5%29%2F%28a%2Bb%29%29%2F%286a%5E2b%5E4%29

Since you aren't trying to find the sum of fractions, you have no need of a Lowest Common Denominator.

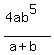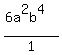So, this is %284ab%5E5%29%2F%28a%2Bb%29 divided by 6a%5E2b%5E4, but the divisor can be expressed as %286a%5E2b%5E4%29%2F1.

Just like performing any other division by a fraction problem, invert the divisor and multiply:



Now, all you need to do is eliminate factors common to both the numerator and denominator, namely 2ab%5E4, leaving you with:

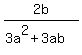%282b%29%2F%28%28a%2Bb%29%283a%29%29 which can be expressed as 2b%2F%283a%5E2%2B3ab%29. It is moot, in my mind, as to which form is simpler. In fact, if this were the result of an intermediate calculation as part of a larger problem, you may choose one over the other depending on the nature of the further calculation in which you intend to use the expression.