Question 174032: Can someone help me graph this please? I have the hardest time with graphing. I can usually figure the problem out, but the graphing is where I struggle. Thank you so much.
Exponential function: Logarithmic function:
f(x)=y=b^x f^-1*(x)=y=logbx
now if b=4 the vertical line is y=4^x and the horizontal line is f(x)=log4x
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
if and only if:

substituting x for y and y for x, the inverse function is therefore:

-----
as you state, if b = 4, then:
exponential equation is:

logarithmic equation is:

-----
since both of these equations are in graphable form, if you have a graphing calculator, you just plug in the formulas:
4^x
and
log(4,x)
and the graphing caculator will take care of if for you.
you just have to make sure you input the formulas correctly for the algorithm that is translating the equation for you.
-----
i'll show you the graph and then give you some words below it.
the graph is:

since these are inverse functions, the solution (a,b) for one equation should be equal to (b,a) for the other equation.
example:
let x = 5
then y = 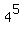 = 1024 = 1024
-----
for the inverse equation,
let x = 1024
then y =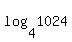 = = 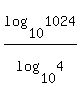 = 5 = 5
-----
your first solution set is: (5,1024)
your inverse solution set is: (1024,5)
-----
this proves these functions are inverse to each other.
-----
to graph manually, since they are both in y = f(x) form, you simply take values for x and solve in each equation:
then you plot the graph.
-----
with your exponential equation, x can be anything.
with your logarithmic equation, x has to be greater than 0.
plot every 5 values of x to see where the equations are going:
first take x = 0:
 = 1: = 1:
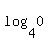 is not possible. is not possible.
then take x = 5:
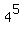 = 1024 = 1024
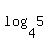 = 1.16... = 1.16...
take x = 10:
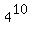 = 1048576 which is off the chart (way up there) = 1048576 which is off the chart (way up there)
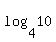 = 1.66... = 1.66...
this is going up much less dramatically.
---
you can take some x points in between to fill it out and get a more accurate representation of what the curve will look like.
if you go minus,
then take x = -5
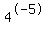 = .000976... = .000976...
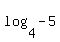 is not possible. is not possible.
-----
what this should be telling you is that as x gets more negative, the exponential equation approaches 0 and the logarithmic equation is not there.
-----
you can see all of this from the graph that i just displayed for you above.
-----
if you don't have a graphing calculator, you can use an online graphing calculator like the one at the following website address:
http://www.e-tutor.com/et3/graphing
this particular calculator can't model log to bases other than 10, but you can use the conversion formula to convert to the base 10.
that conversion formula is:

you separate equations using semi:colon.
for example:
i went to that website and entered the following into the formula section:
4^x;log(x)/log(4)
try it yourself if you have time and interest.
-----
if you wish to see how the formula for the graph was modeled in algebra.com, just look at the source code and look for the keyword "graph".
-----
|
|
|