SOLUTION: A rocket is launched from ground level with an initial velocity of 224ft/s. The height h in ft. of the rocket at any given t in secs. is h(t)= 224t-16t^2. a. when will the rocket

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: A rocket is launched from ground level with an initial velocity of 224ft/s. The height h in ft. of the rocket at any given t in secs. is h(t)= 224t-16t^2. a. when will the rocket      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 173945: A rocket is launched from ground level with an initial velocity of 224ft/s. The height h in ft. of the rocket at any given t in secs. is h(t)= 224t-16t^2.
a. when will the rocket reacha height of 528?
b. When will the rocket reach the ground?
c. When will the rocket reach its maximum height.
d. What is the maximum height of the rocket?
e. Greaph this situation
f. State the domain and range of the graph?
528=224t-16t^2
16t^2 - 224t + 528 = 0
16(t^2 - 14t + 33) = 0
16[(t-3)(t-11)
t-3=0 t-11=0
t=3 t=11
I go back and substitute these numbers in right, to see which one works?
I'm lost after that.
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Your work:
528=224t-16t%5E2
16t%5E2+-+224t+%2B+528+=+0
16%28t%5E2+-+14t+%2B+33%29+=+0
16%28t-3%29%28t-11%29=0
t-3=0 or t-11=0
t=3 or t=11

So far, so good. Remember the rocket goes up, and then comes back down again. What you have discovered so far is that the height is 528 feet 3 seconds after launch, and then it keeps going up. At some point it starts coming back down again, and at 11 seconds after launch it passes 528 feet again.

Part b is exactly the same problem, except that you use 0 instead of 528. You will get two roots for your equation again, one will be 0 because the rocket is on the ground at time 0, and the other will be the time it hits the ground on the way back down.

Part c. Recognize that h(t) will graph as a parabola, concave down. That means the vertex of the parabola is a maximum value. The x-coordinate of the vertex of a parabola expressed in the form 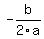y=ax%5E2%2Bbx%2Bc is given by -b%2F2a, so in your case -224%2F-32=7. So maximum height will be reached at 7 seconds. Note that this makes sense because 7 seconds is exactly in the middle of the 3 seconds and 11 seconds you calculated in part a. This gives you a check on your work in part b, because 7 must also be exactly in the middle of 0 and whatever you got from part b.

Part d. Simply evaluate h(7), in other words calculate h%287%29=-16%287%29%5E2%2B224%287%29

Part e.
graph%28600%2C600%2C-1%2C15%2C-50%2C850%2C-16x%5E2%2B224x%29

Part f.

The domain of the function h(t) as stated is all real numbers, but in practical terms, the function is undefined both before the rocket is launched (t<0) and after the rocket hits the ground again, t greater than the value you calculated in part b. Again, purely mathematically speaking, the range is any real number less than the value you calculated in part d. But in practical terms, the height never gets below 0. So you would say that the range is greater than or equal to zero and less than or equal to the value from part d.