Put 1's in front of the single letters
Separate into terms, erasing the plus signs, keeping
the minus signs as negative signs:
Erase all the letters and replace the equal signs
with "|"'s:
Erase the brace and put parentheses around it:
Now we want to end up with a matrix like this,
with three zeros on the the bottom left, and
numbers everywhere else:
Start with this:
Swap the rows so that the smallest number in absolute
value in the first column is on the far left of the
top row. Since 1 is the smallest number in absolute
value in row 1, I will swap rows 1 and 2:
Now we will add 4 times the top row to the 2nd row,
to get a zero where the -4 is. It's easier if you
write 4 to the left of the top row and 1 to the left
of the second row,and write that equal to a new matrix
with the same 1st and 3rd rows, with a blank middle row:
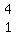
Then you can easily fill in the blank row term by term as:
Since all the numbers in the middle row are divisible by
11, we can multiply it through by 
:
Now we will add 7 times the top row to the 3rd row,
to get a zero where the -7 is. It's easier if you
write 7 to the left of the top row and 1 to the left
of the bottom row,and write that equal to a new matrix
with the same 1st and 2nd rows, with a blank bottom row:
Then you can easily fill in the blank row term by term as:
---
Now we will add -27 times the middle row to 2 times
the 3rd row, to get a zero where the -27 is. It's
easier if you write -27 to the left of the middle row
and 2 to the left of the bottom row,and write that
equal to a new matrix with the same 1st and 2nd rows,
with a blank bottom row:
Then you can easily fill in the blank row term by term as:
The bottom row can be multiplied through by 
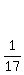
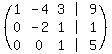Now we put the letters back as we took them out, and
put equal signs where the "|"'s are:
So we have this system:
Now we do what is called "back-substitution":
Substitute 
into the middle equation:
Finally substitute both and 
in
the top equation:
So 
, , .
Edwin
