Question 173475: A food store makes a 9-lb mixture of peanuts. cashews, and raisens. Peanuts cost $1.50 per pound, cashews cost $2.00 per pound, and raisens cost $1.00 per pound. The mixture calls for twice as much peanuts than cashews. The total cost of the mixture is $13.00. How much of each ingredient did the store use?
How do you det this up into equations?
Found 2 solutions by Mathtut, josmiceli:
Answer by Mathtut(3670)   (Show Source):
Answer by josmiceli(19441)  (Show Source):
You can put this solution on YOUR website! These problems are always easier if you put letters in place
of the things you're looking for:
Let  = the pounds of peanuts needed
Let  = the pounds of cashews needed
Let  = the pounds of raisins needed
The 1st sentence says it's a 9-pound mixture, so
(1) 
Peanuts cost $1.50 per pound, so the cost of the peanuts will be
Cashews cost $2.00 per pound, so the cost of the cashews will be
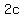
Raisins cost $1.00 per pound, so the cost of the raisins will be
The total cost of the mixture is $13.00, so
(2) 
The mixture calls for twice as much peanuts than cashews, so
(3) 
Now I have 3 equations and 3 unknowns, so it should be solvable
Subtract (1) from (2)
Substitute (3) for
And, going back to (3),
Use (1) to find
The amounts of the ingredients are 2 pounds of cashews,
4 pounds of peanuts, and 3 pounds of raisins
Check answer:
(2)
OK
|
|
|
