Question 173440: Explain when a system of equations will have no solution and when it will have an infinite number of solutions.
Found 2 solutions by Mathtut, solver91311:
Answer by Mathtut(3670)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equations describing the same line
· have an Infinite number of solutions that would be like x+y=3 and 3x+3y=9...these are the same lines
:
Lines that do not intersect (Parallel Lines; having the same slope)
have No solutions
example: y=2/3x+7
........y=2/3x+9
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! The solution set of a linear equation in two variables is a set of ordered pairs such that the coordinates of each pair make the equation a true statement. The solution set of such an equation, if graphed in 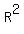 , will describe a straight line. , will describe a straight line.
If you have a system of two equations, there are three possibilities.
1. Consistent system: There is a single ordered pair that is an element of both solution sets. If both equations are graphed in 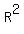 , the result will be two intersecting lines and the point of intersection will be defined by the single ordered pair that is an element of both solution sets, and this single ordered pair is the solution set of the system. , the result will be two intersecting lines and the point of intersection will be defined by the single ordered pair that is an element of both solution sets, and this single ordered pair is the solution set of the system.
2. Inconsistent system: There is no ordered pair that is an element of both solution sets, in other words, the solution set of the system is the empty set. If both equations are graphed in 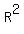 , the result will be two parallel lines. , the result will be two parallel lines.
3. Undetermined system: Every element of the solution set of one of the equations is also an element of the solution set of the other equation. In other words, the solution set for the system is identical to the solution set for either of the lines and therefore has an infinite number of elements. If both equations are graphed in 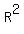 , the result will be that both equations graph to the same line. , the result will be that both equations graph to the same line.
All of these definitions can be extended to systems of equations that are comprised of any number of equations with a like number of variables, except that once you have more than three variables/equations, the graphical analogue becomes impossible to visualize -- we can draw pictures of 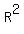 and and 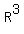 , but , but  and beyond can't be done. and beyond can't be done.
|
|
|