Question 173390: Please help me verify this equation:
cscx - cscx
------ ------ =2sec^2x
1+cscx 1-cscx
yes, the cscx's are over 1+cscx and 1-cscx. Those are fractions.
So far i have gotten stuck on this porblem. i have expanded csc x into 1/sinx in both parts of the left side of the equation which gets me:
1/sinx - 1/sinx
-------- --------- = 2sec^2x
1+1/sinx 1-1/sinx
After that i tried to achieve a common denominator on the left side which is where i get lost. I'm not sure what step to do after that or how to solve it.
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! good one.
maybe i got the answer.
you want to prove this equation is true.
here goes:
-----
let c = csc(x)
let s = sec(x)
-----
your equation becomes:

-----
if you multiply both sides of the equation by (1-c)*(1+c), you get:

-----
simplifying, this becomes:

which becomes:

-----
this is where substitutions come in.
you know that:

you also know that:
sin(x) = 1/csc(x)
and that:
cos(x) = 1/sec(x)
substituting for sin(x) and cos(x), the equation becomes:

if you multiply both sides of this equation by 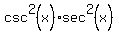 , the equation becomes: , the equation becomes:

subtract 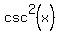 from both sides of this equation to get: from both sides of this equation to get:

simplify this on the right hand side to become:

divide both sides of this equation by 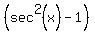 to get: to get:

-----
this is the same as:

and, since we originally let c = csc(x) and we let s = sec(x), this equation now becomes:

-----
we can now substitute for c^2 in the original equation we derived above, which was:

simplifying this, it becomes:

-----
substituting for  , that equation becomes: , that equation becomes:

-----
if we multiply both sides of this equation by  , we get: , we get:

this becomes:

which becomes:

if we multiply both sides of this equation by (-1), it becomes:

which proves that the original equation of:

is true.
-----
since we originally substituted c for csc(x), and s for sec(x), the original equation becomes:

and the proven identify becomes:

-----
|
|
|