Question 172999: For the exponential function e^x and logarithmic function log x, graphically show the effect if x is doubled, can someone help me with the problem, I do not understand what they are asking. Thank you!!!
Found 2 solutions by stanbon, gonzo:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the exponential function e^x and logarithmic function log x, graphically show the effect if x is doubled,
----------------------------------
e^x vs. e^(2x)

----------------------------------
ln(x) vs ln(2x)

=================================
Comment:I can't get this site to graph ln(x) and ln(2x) which is ln(x) + ln(2)
=================================
Cheers,
Stan H.
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! they want to know the impact of doubling x.
i take this to mean:
if you have  and you double x, then you have and you double x, then you have 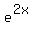
likewise:
if you have 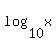 and you double x, then you have and you double x, then you have 
-----
first i will graph  and and 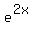 to see what the impact would be: to see what the impact would be:
look below the graph for further comments.
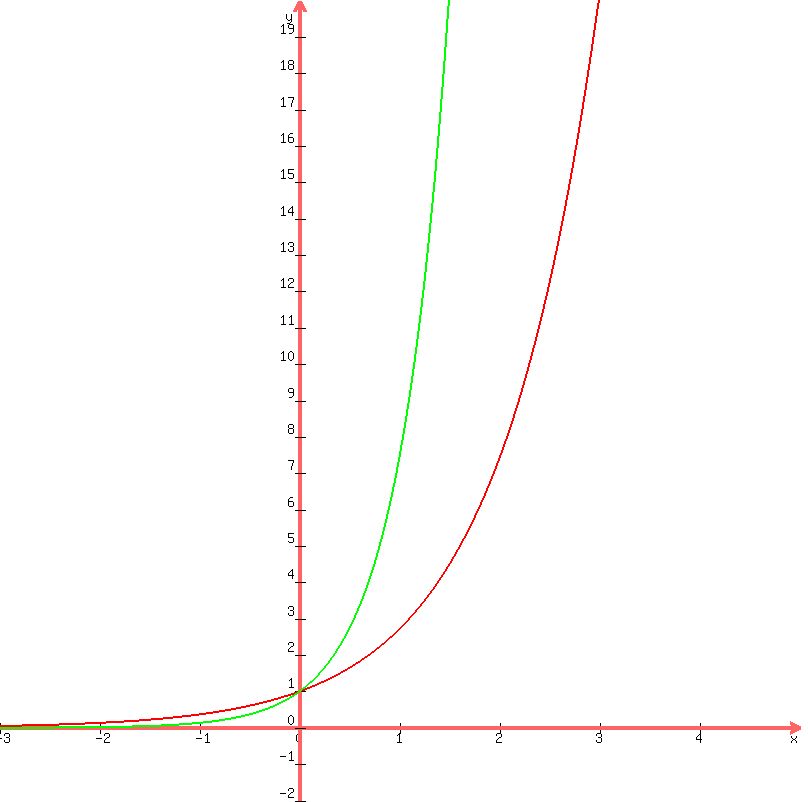
the faster rising curve is 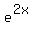
when x = 0, the values of both curves is the same.
when x = 1, the value of  is 2.718... and the value of is 2.718... and the value of 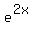 is 7.389... is 7.389...
when x = 2, the value of  is 7.389... and the value of is 7.389... and the value of 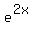 is 54.598... is 54.598...
the value of 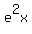 appears to be the value of appears to be the value of 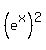 which is should since which is should since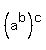 equals equals 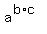 by the laws of exponentiation. by the laws of exponentiation.
-----
when x = -.5,  = .6065 and = .6065 and 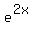 = .3678. = .3678.
 = .3678 so the ratio holds even though = .3678 so the ratio holds even though 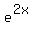 is smaller than is smaller than  at this point. at this point.
---
you can see this on the graph.
-----
the graph of 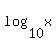 and and  is shown now. is shown now.
look below the graph for further comments.

this graph doesn't show such a dramatic change in the value of log(x) versus log(2x)
example:
when x = 10, log(x) = 1, and log(2x) = 1.301...
when x = 100, log(x) = 2, and log(2x) = 2.301...
when x = 1000, log(x) = 3, and log(2x) = 3.301...
-----
this is because when x is an exponent, it has a very large impact on the result.
when x is the result of exponentiation, it has a very small impact on the result.
when x is the exponent, this is what happens:
if you take x = 1, then 10^1 = 10
if you take x = 10, then 10^10 = 10000000000
there's a big difference.
-----
when x is the result of exponentiation, this is what happens:
if you take x = 1000, then 10^y = 1000 which means y = 3.
if you double x to be 2000, then 10^y = 2000 which means y = 3.301029996
doubling the answers causes a very small increase in the exponent.
-----
y = 10^x means x is the exponent
y = log(x) means x is the answer.
remember:
y = log(x) if and only if x = 10^y
x is the result of exponentiation when you say y = log(x)
x is the exponent itself when you say y = 10^x.
----
best i can do.
hope it makes sense.
-----
|
|
|