Question 172826: Joe has a collection of nickles and dimes that is worth, $7.05. If the # of dimes were doubled, and the # of nicles were increased by eight, the value of the coins would be, $11.75. How many dimes does he have?
It really helps me to understand if I can See each step to solve this problem written out like in a math book. Thank you
Found 3 solutions by checkley77, solver91311, josmiceli:
Answer by checkley77(12844)   (Show Source):
You can put this solution on YOUR website! Let D=the number of dimes.
Let N=the number of nickles.
.10D+.05N=7.05 (multiply this equation by -2 & add to the other equation
.10*2D+.05(N+8)=11.75
.20D+.05N+.40=11.75
.20D+.05N=11.75-.40
.20D+.05N=11.35
-.20D-.10N=-14.10
-----------------------
-.05N=-2.75
N=-2.75/-.05
N=55 nickles.
.10D+.05*55=7.05
.10D+2.75=7.05
.10D=7.05-2.75
.10D=4.30
D=4.30/.10
D=43 dimes.
Proof:
.20*43+.05*55=11.35
8.60+2.75=11.35
11.35=11.35
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website! Let  be the number of dimes and  be the number of nickels.
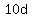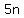That means that the value of his dimes is  cents and the value of his nickels is  cents.
I expressed those values in terms of cents because it is less messy if you don't have to deal with decimal fractions as coefficients in the equations, but the problem would have worked out just as well to say the value of the dimes is  dollars. The only thing you have to remember if you express the value in cents is to change the total value numbers, i.e. $7.05 and $11.75 to 705 cents and 1175 cents.
The first thing we know is that 
Next, if we double the number of dimes, we now have 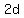 dimes, the value of which is  cents. If we increase the number of nickels by 8, then the value of the nickels becomes  cents.
Now we can say  . Collect like terms and put it in standard form and you get  .
That gives us a system of two equations in two variables that can be solved by a variety of methods. I choose to use the elimination method because I can see that the coefficients in the two equations lend themselves to a tidy solution by using elimination.
Step 1: Multiply by  to get 
Step 2: Add the result of Step 1 to the second equation, namely to get  or, after simplifying,  (Notice how the coefficient on went to zero, effectively eliminating that variable? Hence the name.)
Step 3: Solve for
 telling us that the original number of dimes was 43.
But you aren't quite done yet, even though you have answered the question. We need to check our work to make sure we didn't make some silly mistake.
If the original number of dimes was 43, then there must have been $4.30 in dimes. $7.05 minus $4.30 is $2.75, meaning that there must have been $2.75 worth of nickels. Dividing by $0.05 we get 55, telling us there were 55 nickels to begin with.
If we double the dimes, we get 2 times 43 equals 86 dimes meaning we now have $8.60 worth of dimes, and if we add 8 nickels we get $2.75 plus $0.40 equals $3.15 worth of nickels.
$8.60 plus $3.15 equals $11.75 which was the amount given in the problem. Answer checks. NOW you are done.
Answer by josmiceli(19441)  (Show Source):
|
|
|
