SOLUTION: Find the general term and the 29th term of the sequence <img src="http://i293.photobucket.com/albums/mm56/cool_user2004/5-1.png" alt="Photobucket - Video and Image Hosting"

Algebra ->  Sequences-and-series -> SOLUTION: Find the general term and the 29th term of the sequence <img src="http://i293.photobucket.com/albums/mm56/cool_user2004/5-1.png" alt="Photobucket - Video and Image Hosting"      Log On


   

Question 172791: Find the general term and the 29th term of the sequence


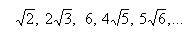
Photobucket - Video and Image Hosting
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Ignoring (for now) the term "6", what do you see happening here?



If we write sqrt%282%29 as 1%2Asqrt%282%29, then we have the sequence

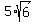
1%2Asqrt%282%29, 2%2Asqrt%283%29, 6, 4%2Asqrt%285%29, 5%2Asqrt%286%29


It looks like the coefficients are increasing by 1 while the radicands (the stuff inside the square root) is 1 more than the coefficients. So if n=1, then the first term is 1%2Asqrt%282%29, and if n=2 the second term is 2%2Asqrt%283%29


So it appears that the sequence is simply a%5Bn%5D=n%2Asqrt%28n%2B1%29 (notice how the radicand is one more than the coefficient).

So take note how 6 is the 3rd term (so n=3). This means that a%5B3%5D=3%2Asqrt%283%2B1%29=3%2Asqrt%284%29=3%2A2=6 (which confirms our answer)


So the sequence is a%5Bn%5D=n%2Asqrt%28n%2B1%29 for n%3E=1


So if, for example, n=4, then the 4th term is a%5B4%5D=4%2Asqrt%284%2B1%29=4%2Asqrt%285%29




To find the 29th term, simply plug in n=29


a%5Bn%5D=n%2Asqrt%28n%2B1%29 Start with the given sequence


a%5B29%5D=29%2Asqrt%2829%2B1%29 Plug in n=29


a%5B29%5D=29%2Asqrt%2830%29 Add


From here, we cannot simplify any further.


So the 29th term is a%5B29%5D=29%2Asqrt%2830%29