|
Question 172712: If you could please help point me in the right direction!!! I need to solve this rational expression:
2 + (4/x-5) = (15/x-4)
I have tried a couple of times, but seem to be off track. I know to find the "LCD" the multiply each side by that... i chose (x-5).
So then i have: [2(x-5)]/1 + [4(x-5)]/(x-5) = [15(x-5)]/(x-4)
I think that is what Im supposed to do, but then I get lost!! Is this the wrong way to apply the "lcd"?
Thank you SO much for your time, Im working on attempt #5... :)
Found 2 solutions by Mathtut, solver91311:
Answer by Mathtut(3670)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm sorry but there is no really nice way to put this except to say that I appreciate you showing the work that you did try. Other than that, your approach isn't even close. So let's get to work.
The process of applying a lowest common denominator involves multiplying all of the fractions by an expression equal to 1 but in such forms that the result is all of the denominators being equal. Let me illustrate with a simple example from arithmetic:
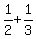 Denominators not equal. The lowest number divisible by both 2 and 3 is 6, so we need, in the case of Denominators not equal. The lowest number divisible by both 2 and 3 is 6, so we need, in the case of  to multiply the denominator by 3 so that the denominator becomes 6. However, if we multiply the denominator by 3, we also have to multiply the numerator by the same number so that we don't change the value of the fraction, thus: to multiply the denominator by 3 so that the denominator becomes 6. However, if we multiply the denominator by 3, we also have to multiply the numerator by the same number so that we don't change the value of the fraction, thus:

Likewise, we change  by multiplying by by multiplying by 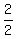 yielding: yielding:

Now that we have 2 fractions with the same value as the original fractions but with equal denominators, we can add them directly:

So let's apply these principles to your problem:

First note that the  factor can also be represented as a fraction factor can also be represented as a fraction 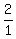 so let's do that: so let's do that:

Now we have three denominators,  , ,  , and , and  . Since none of these expressions are further factorable there are no common factors that we could remove to make the Lowest Common Denominator anything less than the product of the three. So the LCD in this case will be . Since none of these expressions are further factorable there are no common factors that we could remove to make the Lowest Common Denominator anything less than the product of the three. So the LCD in this case will be 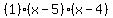 or simply or simply  . You could multiply these two binomials using FOIL, but as you will see, that would be counter-productive at this point -- leave it in the two binomial factor form. . You could multiply these two binomials using FOIL, but as you will see, that would be counter-productive at this point -- leave it in the two binomial factor form.
In order to apply the LCD to the term 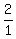 we need to recognize that the factors of the LCD missing from this denominator are both we need to recognize that the factors of the LCD missing from this denominator are both  and and  . Therefore we have to multiply . Therefore we have to multiply 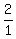 by by 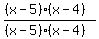 giving us giving us 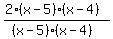 and that is the first term. and that is the first term.
Next we deal with 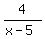 . Here the missing factor is . Here the missing factor is  , so we multiply by , so we multiply by 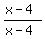 . The second term is therefore . The second term is therefore 
By now you should be able to see that the third term must be 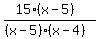
Now let's reconstruct the original equation with the LCD applied:

Since we have an equation, we can multiply both sides of the equation by the same value, so let's use  and voila! the denominators go away completely leaving us with: and voila! the denominators go away completely leaving us with:

Now is a good time to multiply the two binomials and while we are at it, apply
the distributive property all the way across:

Collect like terms and put the resulting quadratic in standard form:

At first blush, this looks like a computational horror, but actually it factors:
 (Verification of this factorization is left as an exercise for the student) (Verification of this factorization is left as an exercise for the student)
So,  or or 
One more consideration that you need to make. It was not a problem in this particular example, but anytime you solve a rational equation, you must check all roots to ensure that they are in the domain of the original function. That means that you cannot have a root that would make the original function undefined. In the case of this example, you would have to exclude either 4 or 5 because either 4 or 5 would give you a zero denominator. Since neither 4 nor 5 is in the solution set for this equation, no problem. But never fail to check when you are solving equations with rational terms.
Hope that helps.
John
|
|
|
| |