Question 172610: solve for x
log4(x-6)+log4x=2
log base 4 (x-6)+log base 4 x=2
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
solve for x

.
If you add to of the same logs together, that is the same thing as multiplying the terms together, with only one log, this is what I mean
.
 = = 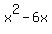
.
The new log would be
.

.
From here we will change this logarthimic equation into an exponential equation
.
This is how you change a logarthmic equation ( logs are a power of a base )
.
 = = 
.
For our equation
.
 = =  = = 
.
Now we can move the "16" to the right and solve the quadratic equation
.
 = =  = =  or or 
.
 , we can factor this equation, , we can factor this equation,
.
( x )(x ), first name all the factors of (-16)
.
One of these pairs will have to add up to (-6)
.
(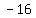 , ,  ) ( added will equal (-15) ) ) ( added will equal (-15) )
.
(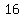 , , 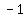 ) ( added will equal "15" ) ) ( added will equal "15" )
.
(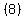 , ,  ) ( added will equal "6") ) ( added will equal "6")
.
( , ,  ) ( added will equal (-6)) ) ( added will equal (-6))
.
You put the highlighted factors into the parentheses with the "x"'s
.
 , you can check by using the foil method, I checked and it is the same as , you can check by using the foil method, I checked and it is the same as 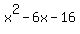
.
You can find "x" by placing both factors equal to "0"
.
 = =  , move the (-8) over to the right side , move the (-8) over to the right side
.
 = =  , , 
.
or
.
 = =  , move the "2" to the right side , move the "2" to the right side
.
 = =  , , 
.
 and and  , the only thing left is to put these values into the original equation, logs can't be nagative, so we need to make sure that our answers don't create negative numbers , the only thing left is to put these values into the original equation, logs can't be nagative, so we need to make sure that our answers don't create negative numbers
.
(x = 8),  = =  = =  ( doesn't make negative, so "8" is a good answer ( doesn't make negative, so "8" is a good answer
.
(x = (-2)),  = =  = =  ( it creates a negative number, so (-2) is no good) ( it creates a negative number, so (-2) is no good)
.
The only answer that works is  , , 
.
The graph of this equation is
.

.
Remember though that "x" can only equal "8", "x" can't be equal to (-2) since this answer made the logs negative
.

.
Hope I helped, Levi
|
|
|