Question 172039: Solve the problem that involves computing expected values in a game of chance.
A game is played using one die. If the die is rolled and shows a 2, the player wins $8. If the die shows any number other than 2, the player wins nothing. If there is a charge of $1 to play the game, what is the game's expected value?
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website! A game is played using one die. If the die is rolled and shows a 2, the player wins $8. If the die shows any number other than 2, the player wins nothing. If there is a charge of $1 to play the game, what is the game's expected value?
There are two possibilities.
1. He wins $7, ($8 - $1 to play), when a 2 is thrown
with probability  .
2. He loses $1, considered as a "negative win", or -$1,
when a 1,3,4,5,or 6 is thrown, with a probability of  .
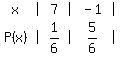
So, the expected value is
 rd of  , or 
That means if you played the game over and over many times,
you would expect to average winning per
game.
Edwin
|
|
|
