|
Question 171849: Please Help! I have five questions I been working on and I am at a stand still. First Question Find an equation of the line having the given slope and containing the given point. m=3(3,2) The equation of the line is y=? (simplify your answer. Use inters or fractions for any number of expression.
The second problem. write an equation of the line containing the given point and perendicular to the given line. (6,7):2x+y=4 The equation of the line is y=?
The third write an equation of the line containing the given point and perpenicular to the given line (7,-8):8x+7y=3 The equation of the line is y=? (type in the form y=mx+b. simplify your answer. type an integer or fraction.
Fourth question Find the equation of the line having the given slope and containing the given point m=3,(3,2)
and fifth question write an equation of the line containing the given point and parallel to the given line. Expressyour answer in the form y=mx+b. (-9,7);5x=7y+9 The equation of the line is y=? Simplify your answer. use integers or fractions for any number in the expression.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Note: I don't mean to be nitpicky, but please use spaces between your problems (as it's hard to find where one problem ends and another begins).
# 1
If you want to find the equation of line with a given a slope of  which goes through the point ( which goes through the point ( , , ), you can simply use the point-slope formula to find the equation: ), you can simply use the point-slope formula to find the equation:
---Point-Slope Formula---
 where where  is the slope, and is the slope, and ) is the given point is the given point
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 
 Add 2 to both sides to isolate y Add 2 to both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line with a slope of  which goes through the point ( which goes through the point ( , , ) is: ) is:
 which is now in which is now in  form where the slope is form where the slope is  and the y-intercept is and the y-intercept is 
Notice if we graph the equation  and plot the point ( and plot the point ( , , ), we get (note: if you need help with graphing, check out this solver) ), we get (note: if you need help with graphing, check out this solver)
 Graph of Graph of  through the point ( through the point ( , , ) )
and we can see that the point lies on the line. Since we know the equation has a slope of  and goes through the point ( and goes through the point ( , , ), this verifies our answer. ), this verifies our answer.
# 2
 Start with the given equation. Start with the given equation.
 Subtract Subtract  from both sides. from both sides.
 Rearrange the terms. Rearrange the terms.
We can see that the equation  has a slope has a slope  and a y-intercept and a y-intercept  . .
Now to find the slope of the perpendicular line, simply flip the slope  to get to get  . Now change the sign to get . Now change the sign to get  . So the perpendicular slope is . So the perpendicular slope is  . .
Now let's use the point slope formula to find the equation of the perpendicular line by plugging in the slope  and the coordinates of the given point and the coordinates of the given point ) . .
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Distribute Distribute
 Multiply Multiply
 Add 7 to both sides. Add 7 to both sides.
 Combine like terms. Combine like terms.
So the equation of the line perpendicular to  that goes through the point that goes through the point ) is is  . .
Here's a graph to visually verify our answer:
 Graph of the original equation Graph of the original equation  (red) and the perpendicular line (red) and the perpendicular line  (green) through the point (green) through the point ) . .
# 3
 Start with the given equation. Start with the given equation.
 Subtract Subtract 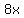 from both sides. from both sides.
 Rearrange the terms. Rearrange the terms.
 Divide both sides by Divide both sides by  to isolate y. to isolate y.
 Break up the fraction. Break up the fraction.
 Reduce. Reduce.
We can see that the equation  has a slope has a slope  and a y-intercept and a y-intercept  . .
Now to find the slope of the perpendicular line, simply flip the slope  to get to get  . Now change the sign to get . Now change the sign to get  . So the perpendicular slope is . So the perpendicular slope is  . .
Now let's use the point slope formula to find the equation of the perpendicular line by plugging in the slope  and the coordinates of the given point and the coordinates of the given point ) . .
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Rewrite Rewrite 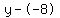 as as 
 Distribute Distribute
 Multiply Multiply
 Subtract 8 from both sides. Subtract 8 from both sides.
 Combine like terms. note: If you need help with fractions, check out this solver. Combine like terms. note: If you need help with fractions, check out this solver.
So the equation of the line perpendicular to  that goes through the point that goes through the point ) is is  . .
Here's a graph to visually verify our answer:
 Graph of the original equation Graph of the original equation  (red) and the perpendicular line (red) and the perpendicular line  (green) through the point (green) through the point ) . .
# 4
This problem is identical to the first question. Make sure that you've entered everything correctly
# 5
 Start with the given equation. Start with the given equation.
 Subract 9 from both sides. Subract 9 from both sides.
 Divide both sides by 7 to isolate y. Divide both sides by 7 to isolate y.
 Rearrange the equation. Rearrange the equation.
 Break up the fraction. Break up the fraction.
We can see that the equation  has a slope has a slope  and a y-intercept and a y-intercept  . .
Since parallel lines have equal slopes, this means that we know that the slope of the unknown parallel line is  . .
Now let's use the point slope formula to find the equation of the parallel line by plugging in the slope  and the coordinates of the given point and the coordinates of the given point ) . .
 Start with the point slope formula Start with the point slope formula
 Plug in Plug in  , ,  , and , and 
 Rewrite Rewrite 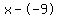 as as 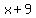
 Distribute Distribute
 Multiply Multiply
 Add 7 to both sides. Add 7 to both sides.
 Combine like terms. note: If you need help with fractions, check out this solver. Combine like terms. note: If you need help with fractions, check out this solver.
So the equation of the line parallel to  that goes through the point that goes through the point ) is is  . .
Here's a graph to visually verify our answer:
 Graph of the original equation Graph of the original equation  (red) and the parallel line (red) and the parallel line  (green) through the point (green) through the point ) . .
|
|
|
| |