|
Question 171810This question is from textbook
: Give the domain of the variable in each expression:
a.
5
-----
2n + 3
b.
5n + 1
------
7
c.
5n + 1
-------
7(2n + 3)
This question is from textbook
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! I'll do the first two to get you going in the right direction.
a)
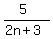 Start with the given expression
 Set the denominator equal to zero. Remember, dividing by 0 is undefined. So if we find values of n that make the denominator zero, then we must exclude them from the domain.
 Subtract 3 from both sides
 Combine like terms on the right side
 Divide both sides by 2 to isolate n
 Reduce
Since makes the denominator equal to zero, this means we must exclude from our domain
So our domain is: 
which in plain English reads: n is the set of all real numbers except n CANNOT equal 
So our domain looks like this in interval notation
\cup\left(\frac{-3}{2},\infty \right))
note: remember, the parenthesis excludes -3/2 from the domain
b)
Looking at 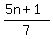 , we can see that there are no square roots, logs, and other functions where there are restrictions on the domain.
Also, we can see that the function does not have a division by n (or any combination of variables and constants).
So we don't have to worry about division by zero.
Since we don't have any restrictions on the domain, this shows us that the domain is all real numbers. In other words, we can plug in any number in for n
So the domain of the function in set-builder notation is:
In plain English, this reads: n is the set of all real numbers (In other words, n can be any number)
Also, in interval notation, the domain is:
)
|
|
|
| |
