SOLUTION: How would I write three quadratic equations, with a, b, and c (coefficients of x2, x, and the constant) as: Integers Rational numbers Irrational numbers

Algebra ->  Equations -> SOLUTION: How would I write three quadratic equations, with a, b, and c (coefficients of x2, x, and the constant) as: Integers Rational numbers Irrational numbers      Log On


   

Question 171526: How would I write three quadratic equations, with a, b, and c (coefficients of x2, x, and the constant) as:
Integers
Rational numbers
Irrational numbers
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
You need to write three equations of the form ax%5E2%2Bbx%2Bc=0

Integers are whole numbers, either positive or negative. -4, 5, and 23 are integers, for example. 0 (zero) is also an integer.

Rational numbers are numbers that can be expressed as the quotient of two integers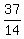. -3%2F4, 1%2F2, and 37%2F14 are rational numbers (all integers are also rational, by the way)

Irrational numbers are any real numbers that CANNOT be expressed as the quotient of two integers. 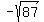sqrt%282%29, -sqrt%2887%29, pi, and e (the base of the natural logarithms) are irrational numbers.

In each case, pick any numbers you like within the given constraints for the caracter of the coefficients, and substitute them for a, b, and c in ax%5E2%2Bbx%2Bc=0