Question 171279: One hose can fill an empty tank in 7 hours. A second hose can fill the empty tank in 12 hours. How long will it take to fill the empty tank if both hoses are used? Write an equation and solve.
Found 2 solutions by midwood_trail, solver91311:
Answer by midwood_trail(310)   (Show Source): (Show Source):
You can put this solution on YOUR website! One hose can fill an empty tank in 7 hours. A second hose can fill the empty tank in 12 hours. How long will it take to fill the empty tank if both hoses are used? Write an equation and solve.
1/7 + 1/12 = 1/x
Can you solve for x?
====================
I received your reply.
1/7 + 1/12 = 1/x
Multiplying all terms on both sides by the LCD, which is 84x, we get the following:
12x + 7x = 84
We now have a linear equation.
So, solve for x.
19x = 84
x = 84/19
x is approximately 4.42, which can be rounded off to the nearest tenths place to be 4.40 (about 4 hours and 40 minutes).
Together, both hoses can fill the empty tank in 4 hours and 40 minutes (slightly less than 5 hours).
Did you follow?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! One of the hoses can fill the tank in 7 hours, so that hose can fill  of the tank in one hour. Likewise, the other hose can fill of the tank in one hour. Likewise, the other hose can fill  of the tank in one hour. of the tank in one hour.
Using both hoses, you can fill  of the tank in one hour. of the tank in one hour.
Therefore, both hoses can fill the tank in 84/19 hours, or just under 4 and a half hours (you can go ahead and calculate the hours, minutes, and seconds if you are so inclined).
In general, for two entities performing work, if entity 1 can do the entire job in  hours and entity 2 can do the entire job in hours and entity 2 can do the entire job in  hours, then both working together can do the job in hours, then both working together can do the job in 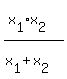 hours. hours.
This is extensible to as many entities as you like simply by adding factors to the numerator and terms to the denominator. For example, with three entities, the formula is:

|
|
|