|
Question 170193: Add. Simplify if possible. 7v/v^2-49 + v/v-7 (this is a fraction)
Find the polynomial for the perimeter and for the area z+8 (top of square) z (side of square).
Subtract by simiplifying collecting like radical terms if possible 4 square root sign 80 - 6 square root sign 5.
If the sides of a square are lengthened by 7cm, the area becomes 196cm^2.
Find the length of a side of the oringinal square.
Please help I have to submit by tomorrow.
Thank you in advance
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
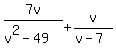 Start with the given equation Start with the given equation
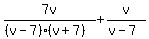 Factor the first denominator Factor the first denominator
Take note that the LCD is 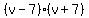
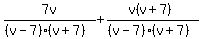 Multiply the second fraction by Multiply the second fraction by 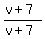 to make the denominators equal. to make the denominators equal.
 Distribute Distribute
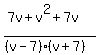 Combine the fractions. Combine the fractions.
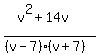 Combine like terms. Combine like terms.
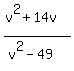 FOIL the denominator. FOIL the denominator.
So 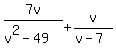 simplifies to simplifies to 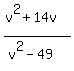
# 2
Area: 
So the area is  square units square units
Perimeter: 
So the perimeter is  units units
# 3
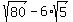 Start with the given expression Start with the given expression
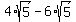 Simplify Simplify 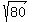 to get to get  . Note: If you need help with simplifying square roots, check out this solver. . Note: If you need help with simplifying square roots, check out this solver.
Since we have the common term  , we can combine like terms , we can combine like terms
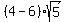 Combine like terms. Remember, Combine like terms. Remember, 
 Now simplify Now simplify 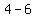 to get to get 
So 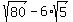 simplifies to simplifies to  . .
In other words, 
# 4
Area of original square 
Area of new square: 
Since the "area becomes 196cm^2", this means that 
 Start with the second equation Start with the second equation
 Plug in Plug in 
 FOIL FOIL
 Subtract 196 from both sides. Subtract 196 from both sides.
 Combine like terms. Combine like terms.
Notice we have a quadratic equation in the form of 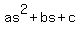 where where  , ,  , and , and 
Let's use the quadratic formula to solve for s
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get  . .
 Multiply Multiply 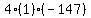 to get to get 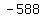
 Rewrite Rewrite  as as 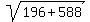
 Add Add  to to  to get to get 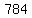
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 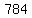 to get to get 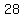 . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible answers are  or or 
However, since a negative side length is NOT possible, this means that the only answer is 
====================================================================
Answer:
So the original side length is 7 centimeters
|
|
|
| |