Question 170094: Please help me, I don't understand!
Find the equation for each of the following items below:
a. A line that passes through (6,2) and has a slope of 2.
b. A line that passes though the points (2,4) and (8,16)
c. A line that passes through (7,3) and has a slope of -1.
d. A line that passes through (1, 1) and is perpendicular to the line 3x+4Y=12.
e. A circle with a radius of 9 and a midpoint at (3,3)
Found 2 solutions by stanbon, Earlsdon:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation for each of the following items below:
a. A line that passes through (6,2) and has a slope of 2.
Line equation y = mx + b; find m and b.
m = 2
b: 2 = 2*6 + b
b = -10
Equation: y = 2x - 10
--------------------------------------
b. A line that passes though the points (2,4) and (8,16)
Line equation y = mx + b; find m and b
m = [16-4]/[8-2] = 2
b: 4 = 2*2 + b
b = 0
Equation: y = 2x
=======================
c. A line that passes through (7,3) and has a slope of -1.
same procudure as above
-----------------------------
d. A line that passes through (1, 1) and is perpendicular to the line 3x+4Y=12.
Find slope of give line: 4y = -3x + 12; y = (-3/4)x + 3
Its slope is -3/4 so the perpendicular line has m = 4/3
b: 1= (4/3)*1 + b
b = -1/3
Equation: y = (4/3)x - (1/3)
-----------------------------
e. A circle with a radius of 9 and a midpoint at (3,3)
(x-3)^2 + (y-3)^2 = 9^2
================================
Cheers,
Stan H.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) Start with the "slope-intercept" form of a linear equation:
y = mx+b where the slope, m = 2 so now you have:
y = 2x+b Now you need to find b, the y-intercept. Substitute the coordinates of the given point through which the line passes (6, 2).
2 = 2(6)+b Solve for b.
2 = 12+b Subtract 12 from both sides.
-10 = b Now you can write the final equation:
y = 2x-10
-------------------
b) First, find the slope using the slope formula:
Remember that the slope is defined as "rise over run" or the difference in the y-coordinates over the difference in x-coordinates.
 Substitute: (2, 4) and (8, 16) Substitute: (2, 4) and (8, 16)



Now you can start the equation with:
y = mx+b and substitute m = 2.
y = 2x+b To find b, substitute the x- and y-coordinates of either one of the two given points. Let's use the point (2, 4), so we get:
4 = 2(2)+b
4 = 4+b
b = 0
The final equation is:
y = 2x
--------------
c) Use the work in a) as a guide for solving this one.
-----------------
d) Find the slope by recalling that perpendicular lines have slopes that are the negative reciprocal of each other.
In othe words, in perpendicular lines, the product of the slopes is always equal to -1.
So, the slope of the line in the given equation (3x+4y = 12) is found by converting the equation to the "slope-intercept" form (y = mx+b) and reading the slope directly from the resulting equation.
 Subtract 3x from both sides. Subtract 3x from both sides.
 Divide both sides by 4. Divide both sides by 4.
 So, by inspection, you can see that the slope is So, by inspection, you can see that the slope is 
But the perpendicular line would have a slope that is the negative reciproacal of 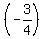 which would be which would be  , so... , so...
 Now you can find b by substituting the x- and y-coordintes of the given point (1, 1) through which the line passes. Now you can find b by substituting the x- and y-coordintes of the given point (1, 1) through which the line passes.
 Subtract Subtract  from both sides. from both sides.
 The final equation is: The final equation is:

---------------------
Starting with the general form of an equation of a circle with its center at (h, k) and a radius of r:
 Substitute (3, 3) for (h, k) and 9 for r Substitute (3, 3) for (h, k) and 9 for r


|
|
|