|
Question 170002: Solve by substitution or elimination method:
3x - 2y = 8
-12x + 8y = 32
Solve by substitution or elimination method:
7x - 5y = 14
-4x + y = 27
Solve by substitution or elimination method:
-4x + 3y = 5
12x - 9y = -15
Found 2 solutions by jim_thompson5910, Electrified_Levi:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Solve by substitution or elimination method:
.
3x - 2y = 8
-12x + 8y = 32
.
Solve by substitution or elimination method:
.
7x - 5y = 14
-4x + y = 27
.
Solve by substitution or elimination method:
.
-4x + 3y = 5
12x - 9y = -15
.
First we will solve the first system with substitution
.
3x - 2y = 8
-12x + 8y = 32
.
First we need to solve for a variable in one of the two equations, doesn't matter which letter, or equation, we will solve for "y" in the first equation
.
 , we will move (-2y) to the right side , we will move (-2y) to the right side
.
 = =  = =  , now we need to move "8" to the left side , now we need to move "8" to the left side
.
 = =  = =  , to find "y" we need to divide each side by "2" , to find "y" we need to divide each side by "2"
.
 = =  = = 
.
 , since "y" is equal to , since "y" is equal to 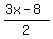 , we can replace "y" in the other equation with , we can replace "y" in the other equation with 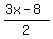 , then just solve for "x" , then just solve for "x"
.
 = =  , now just solve for "x" , now just solve for "x"
.
 = =  = =  , now we will use the distribution method , now we will use the distribution method
.
 = = 
.
Remember the + and - signs,  , adding the "x"'s , adding the "x"'s
.
 = =  = =  ( False ) ( False )
.
This means ( when the x's or y's cancel out, and there is a false statement) that there are no solutions, these lines are parallel, there is no intersection, and therefore no solutions
.
Here is the graph of this system
.

.
Now we will solve the second system, by elimination
.
7x - 5y = 14
-4x + y = 27
.
Elimination is when you add the two equations together, and it gets rid of a variable, first we need to make sure the x's or y's in each equation are the same, or the negative of the other
.
We can eliminate any variable ( either x or y )
.
We will get rid of the y's
.
We need to either get both y's to "5y" or "-5y" or we need to get them to "y" or "-y", we will change the second equation to "5y"
.
 , to get "y" to change to "5y" we need to multiply each side by (5) , to get "y" to change to "5y" we need to multiply each side by (5)
.
 = =  = = 
.
We will need to use the distribution method
.
 = =  = = 
.
Remember the signs,  , this is our new equation , this is our new equation
.
Now we will bring the firt equation to our second new equation
.

.

.
We will now add the equations
.

.

.
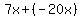 = = 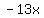
.
 = = 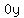 = = 
.
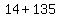 = = 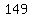
.
It will become  = =  , to find "x" we need to divide each side by , to find "x" we need to divide each side by 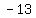
.
 = =  = =  = =  , we can now replace "x" with , we can now replace "x" with 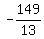 , in one of the two original equations , in one of the two original equations
.
7x - 5y = 14
-4x + y = 27
.
We will use the second equation
.
 = =  = =  = = 
.
Now we need to move 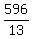 to the right side ( we will convert "27" into "13ths" to the right side ( we will convert "27" into "13ths"
.
 = =  = =  = =  = = 
.
 , we can check our answers by replacing "x" and "y" in both original equations , we can check our answers by replacing "x" and "y" in both original equations
.

.

.
First equation,  = =  = =  = =  = =  = =  = =  ( True ) ( True )
.
Second equation,  = =  = =  = =  = =  = =  , ( True ) , ( True )
.

.

.
Solution sets are in the form (x,y), our solution set is ( 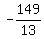 , , 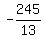 ) )
.
The graph of the system is
.

.
The intersection is your answer
.
Now we can do the last system
.
-4x + 3y = 5
12x - 9y = -15
.
We will use the elimination method of solving this problem
.
Remember elimination is where you get rid of a variable
.
We will multiply the first equation by "3" to get rid of the "y"
.
 = =  = =  we will use distribution we will use distribution
.
 = =  = = 
.
Remember signs,  , now we can add the new first equation to the second equation , now we can add the new first equation to the second equation
.

.

.
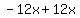 = = 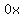 = = 
.
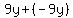 = = 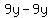 = = 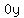 = = 
.
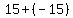 = = 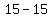 = = 
.
It will become  = =  (True) (True)
.
This means ( when both x and y cancel out, and there is a true statement) that this is the same line, both equation will be one line, there is an infinite number of solutions ( since the equations are equal to one line )( or the second line is put on the first line )
.
Here is the graph of this system
.

.
Your answers are
.
First system of equations = " no solutions " ( since they are parallel lines )
.
Second system of equations = ( 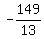 , , 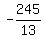 ) ( the lines intersect at point ( ) ( the lines intersect at point ( 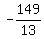 , , 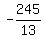 ) )
.
Third system of equations = " infinite solutions " ( since the two equations are the same line )
.
Hope I helped, Levi
|
|
|
| |