|
Question 169955: By looking at two linear equations, is there a way you can tell if the corresponding lines are parallel?
Found 3 solutions by ankor@dixie-net.com, solver91311, ellimery:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! By looking at two linear equations, is there a way you can tell if the corresponding lines are parallel?
:
Parallel lines have the same slope
:
Ensure that the equations, in the point/slope form (y = mx + b)
:
If m is the same in both equations, the slopes are equal and the lines are parallel
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! That depends a great deal on the complexity (or lack thereof) of the equations and your own mental calculation skills.
First of all, I have to presume that you are dealing with two-variable equations.
Given that, if they are in slope-intercept form ( ), determining parallelism is very easy. If the value of ), determining parallelism is very easy. If the value of  in both equations is the same and the value of in both equations is the same and the value of  is different, you have two parallel lines. If the value of is different, you have two parallel lines. If the value of  is also the same in both equations, you have two representations of the same line. If the two is also the same in both equations, you have two representations of the same line. If the two  values are different, then the lines are not parallel. values are different, then the lines are not parallel.
If the equations are in standard form ( ), you have to do a little mental arithmetic. Look at the fraction ), you have to do a little mental arithmetic. Look at the fraction  reduced to lowest terms for each of the equations. If different, then the lines are not parallel. If the same, you have to look at the fraction reduced to lowest terms for each of the equations. If different, then the lines are not parallel. If the same, you have to look at the fraction 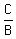 reduced to lowest terms for each equation to determine if the lines are parallel or the same line. reduced to lowest terms for each equation to determine if the lines are parallel or the same line.
Examples:


 for the first equation is for the first equation is 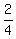 which reduces to which reduces to 
 for the second equation is for the second equation is 
They are the same, so you potentially have parallel lines.
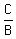 for the first equation is for the first equation is  which reduces to which reduces to 
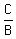 for the second equation is for the second equation is 
They are also the same so the lines are the same line, not parallel lines
On the other hand if you had started with:


 for the first equation is for the first equation is 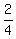 which reduces to which reduces to 
 for the second equation is for the second equation is 
They are the same, so you potentially have parallel lines.
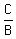 for the first equation is for the first equation is  which reduces to which reduces to 
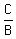 for the second equation is for the second equation is  which reduces to which reduces to 
They are NOT the same, so you do have parallel lines in this case.
For the third case, presume you start with:


 for the first equation is for the first equation is 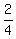 which reduces to which reduces to 
 for the second equation is for the second equation is 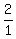 which reduces to which reduces to 
They are NOT the same, so the lines are not parallel and intersect in exactly one point.
The examples given were very simple in terms of the character of the coefficients. Large number coefficients, fractional coefficients (decimal or otherwise), and irrational coefficients may stretch the ability of some folks to do the calculations mentally. The point is that virtually no one would be able to determine parallelism for ANY pair of two-variable linear equations, but for the types of problems that are presented in a typical first-year Algebra course, the above method should suffice in the vast majority of cases.
Of course, once you add the complexity of a third variable, all bets are off. In the first place, you now have four possiblities: The lines can be parallel, they can be the same line, they can be 'skew' lines (the lines themselves are not parallel, but lie in parallel planes), or they just might intersect in a single point. Four or more variables, the idea of parallelism no longer applies because you can't draw a picture in four or more dimensions.
Hope this helps.
John
Answer by ellimery(1)   (Show Source): (Show Source):
You can put this solution on YOUR website! March 14, 2010
Math 208 Week 4 DQ 2
By looking at two linear equations, how can you tell that the corresponding lines are parallel?
The first thing to look at when trying to figure if an equation is going to be parallel we must look at it in slope- intercept form (Y=MX+B), this will allow the determination of parallelism come easily. So if the value in the M spot is the same and the value of B is different this shows itís a parallel line. If the equation is given in standard form (AX+BY=C) you will have to look at it as a fraction so A/B reduced to its simplest form for both of the equations. If these lines are different then they are not parallel, if the same they are. While doing this we also have to look at C/B reduced to its simplest form to determine if it is parallelism.
Examples:
2X + 4Y = 6
X+ 2Y = 3
A/B for the first equation is 2/4 which reduces to 1/2
A/B for the second equation is 1/2
They are the same, so you potentially have parallel lines.
C/B For the first equation is 6/4 which reduces to 3/2
C/B For the second equation is 3/2
they are also the same so the lines are the same line, not parallel lines
|
|
|
| |