Find the domain and range of the inverse of the function.
 Let's do it graphically first, and then we'll do it
algebraically.
First we'll draw the graph of
Let's do it graphically first, and then we'll do it
algebraically.
First we'll draw the graph of 
 That is a parabola with vertex (0,6).
However because of the
That is a parabola with vertex (0,6).
However because of the  restriction, we will have to eliminate
the left half of the graph to have the
graph of f(x), which is this:
restriction, we will have to eliminate
the left half of the graph to have the
graph of f(x), which is this:
 The domain of
The domain of  is
is 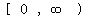 The range of
The range of  is
is 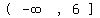 Now let's draw what is called "the identity line",
which is the 45°-line through the origin whose
equation is
Now let's draw what is called "the identity line",
which is the 45°-line through the origin whose
equation is  . I'll draw the identity line
in green dotted:
. I'll draw the identity line
in green dotted:
 Now let's draw the graph of
Now let's draw the graph of 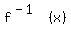 ,
the inverse of
,
the inverse of  by reflecting it across the
green dotted identity line like this:
by reflecting it across the
green dotted identity line like this:
 The domain of
The domain of  is
is 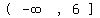 The range of
The range of  is
is 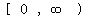 Notice that the range of
Notice that the range of  is the domain of
is the domain of 
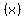 ,
and the domain of
,
and the domain of  is the range of
is the range of 
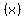 .
That's doing it graphically. Now let's do it
algebraically:
.
That's doing it graphically. Now let's do it
algebraically:
 Replace
Replace  by
by 
 Interchange
Interchange  and
and  :
:
 Solve for y:
Solve for y:
 We take the square roots of both sides, and
since
We take the square roots of both sides, and
since  , we do not need "±".
, we do not need "±".
 Now we replace
Now we replace  by
by 
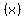
 What is under the square root radical must not be negative,
so
What is under the square root radical must not be negative,
so  or
or  or
or  So, because of
So, because of  ,
The domain of
,
The domain of  is
is 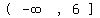 and because of the
and because of the  ,
The range of
,
The range of  is
is 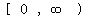 Edwin
Edwin