Question 169705: This is one main word problem/question broken down into several questions. Post a response to the following: How do you know if a quadratic equation will have one, two, or no solutions? How do you find a quadratic equation if you are only given the solution? Is it possible to have different quadratic equations with the same solution? Explain. Provide your classmate’s with one or two solutions with which they must create a quadratic equation.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! A quadratic equation will ALWAYS have two solutions. However, they can be:
2 real and equal solutions (also expressed as one real solution with a multiplicity of 2)
2 real and unequal solutions, or
2 complex solutions
If the discriminant (the part under the radical in the quadratic equation, i.e. the  part) is: part) is:
 , then you have 2 real and equal solutions , then you have 2 real and equal solutions
 , then you have 2 real and unequal solutions , then you have 2 real and unequal solutions
 , then you have a pair of conjugate complex roots of the form: , then you have a pair of conjugate complex roots of the form:
 and and 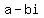 where where  is the imaginary number defined by is the imaginary number defined by 
If the solutions to a quadratic equation are p and q, then you can write:
 , then apply FOIL to multiply the two binomials to obtain your quadratic , then apply FOIL to multiply the two binomials to obtain your quadratic 
There are an infinite number of quadratic equations that can be represented by a given pair of solutions.  is one quadratic with solutions p and q, but is one quadratic with solutions p and q, but  is a different quadratic, and is a different quadratic, and  represents a set of quadratic equations with a set element, each different from the others, for every possible value of a. represents a set of quadratic equations with a set element, each different from the others, for every possible value of a.
Example (real/unequal):
Let  and and  be solutions of a particular quadratic equation. be solutions of a particular quadratic equation.
Then  is a quadratic equation with the given solutions as roots. is a quadratic equation with the given solutions as roots.
Example (real/equal):
Let  and and  be solutions of a particular quadratic equation. be solutions of a particular quadratic equation.
Then  is a quadratic equation with the given solutions as roots. is a quadratic equation with the given solutions as roots.
Example (complex)
Let  and and  be solutions of a particular quadratic equation. be solutions of a particular quadratic equation.
Then  is a quadratic equation with the given solutions as roots. is a quadratic equation with the given solutions as roots.
Hope that helps
|
|
|