|
Question 169690This question is from textbook
: Estimate the one-sided limits for the function:
f(x) = 17 - x/(x-8)^2
lim f(x) when x approaches 8+
and
lim f(x) when x approaches 8-
This question is from textbook
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
-----
limit as x approaches +8:
f(x) approaches 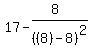
which becomes:
f(x) approaches 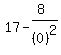
which becomes:
f(x) approaches 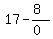
which becomes:
f(x) approaches 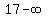
which becomes:
f(x) approaches 
-----
ax x approaches 8, denominator would approach 0
this would cause the numerator to approach infinity.
this would cause 17 minus the numerator to approach minus infinity.
-----
example:
let x = 7.999999999
this is pretty close to 8 but not as close as you can get but the calculator only goes up 9 digits so i used this as an example.
-----
x/(x-8)^2 = 7.999999999 * 10^18
that number is so large, that scientific notation was required to display it.
multiplying by 10^18 means moving the decimal point to the right 18 places.
the number is around 8,000,000,000,000 which means around 8 trillion.
17 - 7.999999999 * 10^18 = -7.999999999 * 10^18
that's pretty close to minus 8 trillion.
in other words, the numerator is so large that the 17 becomes insignificant and can be discounted.
-----
i would have to say that as x approaches +8, f(x) approaches -
-----
limit as x approaches -8:
since this doesn't cause the denominator to be 0, you don't need to take the limit as x approaches, but can actually calculate the value of f(x) when x = -8.
f(x) = 17 - x/(x-8)^2
f(-8) = 17 - (-8)/(-8-8)^2
= 17 - (-8)/(-16)^2
= 17 - (-8)/(+256)
= 17 - (-.03125)
= 17 + .03125
= 17.03125
-----
|
|
|
| |