Question 169002This question is from textbook college algebra
: can somebody help me solve this equation:  This question is from textbook college algebra
This question is from textbook college algebra
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
can somebody help me solve this equation: 
.
first we must take the log of both sides, log is the inverse function of an exponent, it is also the power of a base function
.
The two sides will have a base of "10"
.

.
 , if there is an exponent in a log such as (x+2), and (x-2), you take the exponents and multiply them by ( , if there is an exponent in a log such as (x+2), and (x-2), you take the exponents and multiply them by (
.
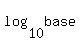 ), in this case ), in this case 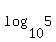 , and , and 
.
 , ,
.
We can rearrange the two sides
.
 = = 
.
we can use the distribution to multiply the numbers out
.
 = =  = = 
.
Remember the signs
.
 , ,
.
now we need to get all the "x"s on one side, we will move 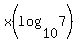 , to the left side , to the left side
.
 = =
.
 = =
.

.
Now we will move 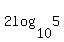 to the right side to the right side
.
 = =
.
 = =
.

.
We can take out the "x"s on the left side ( since they both have it in common
.
 = = 
.
To find "x" you would divide both sides by 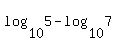
.
 = =  = =
.
 = = 
.
 = =  (rounded)(you have to solve using a calculator) (rounded)(you have to solve using a calculator)
.
You usually check by replacing "x" with the answer, but in this case, it would be hard since the answer never stops ( I checked it, and it is right )
.
Hope I helped, Levi
|
|
|