|
Question 168985: parallel, perpendicular or neither:
y=x+7
y=-x+2
Found 2 solutions by checkley77, Electrified_Levi:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! Because the slopes are negative recipricals of each other then these lines are perpendicular.
y=x+7 (red line)
y=-x+2 (green line)
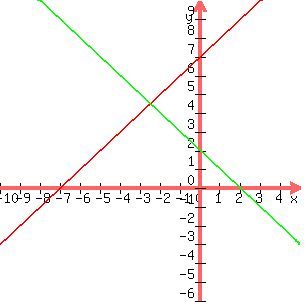 (graph 300x300 pixels, x from -10 to 5, y from -6 to 10, of TWO functions x +7 and -x +2). (graph 300x300 pixels, x from -10 to 5, y from -6 to 10, of TWO functions x +7 and -x +2).
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
parallel, perpendicular or neither:


.
These equations are in the form of  , where "m" is the slope, "b" is the y intercept , where "m" is the slope, "b" is the y intercept
.
The slope of the first line is "1"
The slope of the second line is (-1)
.
If lines are parallel, their slopes would be the same, these lines are not parallel
.
If lines are perpendicular, their slopes will be the negative reciprocal of each other
.
Reciprocal of the first slope would be  , if you put a negative on it, it would be , if you put a negative on it, it would be 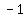 , which is equal to the second slope , which is equal to the second slope
.
Reciprocal of the second slope would be 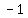 , if you put a negative on it, it would be , if you put a negative on it, it would be  , which is the first slope , which is the first slope
.
These lines are perpendicular ( the numbers after the slopes don't matter, in finding if lines are parallel, perpendicular, or neither ) ( the numbers after the slopes are where the lines cross the y axis )
.
Here is the graph of the two lines
.

.
Hope I helped, Levi
|
|
|
| |