Question 168877This question is from textbook Intermediate Algebra
: Please Help Me.
I need an IN DEPTH EXPLANATION OF HOW TO SOLVE THIS PROBLEM.
This question was answered but I was not given an full explanation. The work was not shown. I need to understand how to get the answer step by step.
Otis Taylor has a box of coins that he uses when playing poker with his friends. The box currently contains 44 coins, consisting of pennies, dimes, and quarters. The number of pennies is equal to the number of dimes, and the total value is $4.37. How many of each denomination of coin does he have in the box?
This question is from textbook Intermediate Algebra
Found 2 solutions by checkley77, ankor@dixie-net.com:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! P=D
P+D+Q=44
D+D+Q=44
2D+Q=44
Q=44-2D
.25Q+.10P+.01D=4.37
.25(44-2D)+.10D+.01D=4.37
11-.50D+.10D+.01D=4.37
-.39D=4.37-11
-.39D=-6.63
D=-6.63/-.39
D=17 NUMBER OF DIMES & PENNIES.
Q=44-2*17
Q=44-34
Q=10 NUMBER OF QUARTERS.
PROOF:
.25*10+.10*17+.01*17=4.37
2.50+1.70+.17=4.37
4.37=4.37
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Otis Taylor has a box of coins that he uses when playing poker with his friends.
The box currently contains 44 coins, consisting of pennies, dimes, and quarters.
The number of pennies is equal to the number of dimes, and the total value is $4.37.
How many of each denomination of coin does he have in the box?
:
p = no. of pennies
d = no. of dimes
q = no. quarters
:
Write an equation for each statement:
:
"The box currently contains 44 coins, consisting of pennies, dimes, and quarters."
p + d + q = 44
:
"The number of pennies is equal to the number of dimes,"
p = d
:
" and the total value is $4.37."
.01p + .10d + .25q = 4.37
:
How many of each denomination of coin does he have in the box?
:
We want to eliminate q here.
Multiply the above equation by 4 and subtract from the total no. of coins eq:
1.0p + 1.0d + 1.0q = 44.00
.04p + .40d + 1.0q = 17.48
--------------------------- subtraction eliminates q
.96p + .60d + 0 = 26.52
:
Remember that p = d, therefore substitute d for p and find d
.96d + .60d + = 26.52
1.56d = 26.52
d = 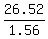
d = 17 dimes
and
p = 17 pennies
:
Find Q:
17 + 17 + q = 44
34 + q = 44
q = 44 - 34
q = 10 quarters
:
:
Check solution in the $ equation
.01(17) + .10(17) + .25(10) =
.17 + 1.70 + 2.50 = 4.37
:
:
Was this enough depth for you?
|
|
|